Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 11
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Esse módulo com o negativo pode até parecer novidade, mas sinais negativos dentro de módulos podem ser manipulados numa boa, saca só:
E como o módulo da multiplicação é a multiplicação dos módulos:
E esse módulo de não tá fazendo nada aí, já que . Daí podemos concluir que:
Vamos usar essa nova equação como a nossa função, já que ela encaixa direitinho com a definição de um módulo deslocado em . Essa daqui ó:
Passo 2
O domínio da nossa função será todos os números reais, já que a função módulo não restringe o domínio.
Passo 3
A imagem da nossa função será todo valor não negativo, já que tudo que entra no módulo sai positivo.
Passo 4
E o nosso gráfico vai ser o módulo do jeito que a gente conhece, só que deslocado no eixo . É só fazer na nossa definição de módulo e o gráfico sai num instante ;)
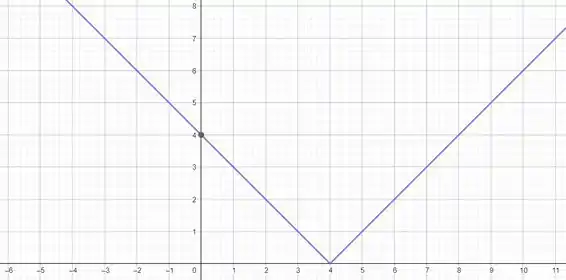
Resposta
Domínio:
Imagem:
