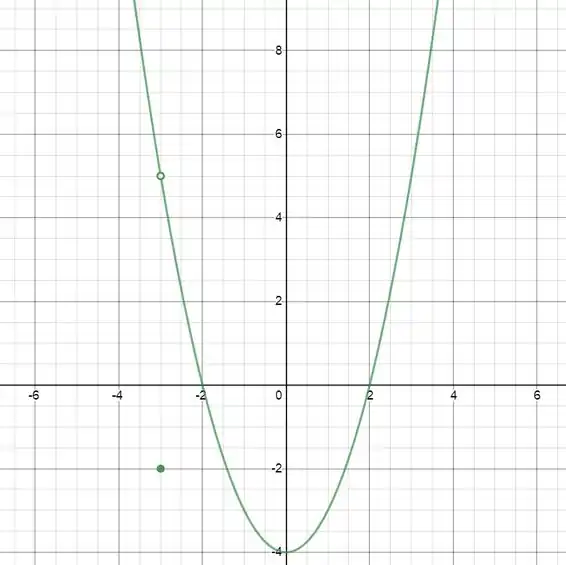
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Primeiro vamos definir o domínio, ou seja, os valores de que estão definidos na função. A função está definida para todos os reais! Ela só muda o comportamento em , mas isso não muda nada em nosso domínio.
Passo 2
A imagem da nossa função precisa de uma percepção um pouquinho mais apurada. Perceba que na primeira condição da função temos , e funções quadráticas são sempre não negativas. Então:
Subtraindo de ambos os lados:
Ou seja:
Mas se lembre que por esse critério precisamos excluir o valor da função em da imagem da função, já que em a função se comporta diferentemente. Fazendo
Da 1ª equação temos então a imagem:
E da 2ª equação vamos ficar com o único valor que assume: . Mas esse valor já está incluso na imagem por conta da imagem da 1ª equação. Então a imagem da nossa função fica .
Passo 3
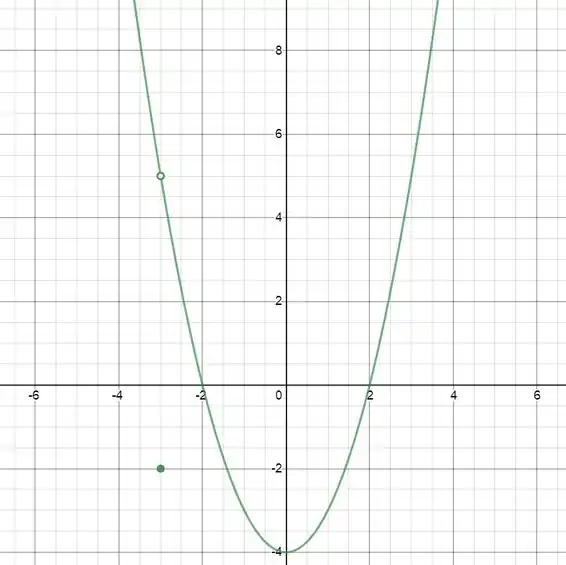
O gráfico será uma parábola deslocada unidades em com exceção do ponto que será substituído pelo ponto . Ficamos com o gráfico:
Resposta
Domínio:
Imagem: