Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 74

Prove analiticamente que o segmento de reta que liga os pontos médios de qualquer par de lados de um triângulo é paralelo ao terceiro lado e seu comprimento é a metade do comprimento do terceiro.

Passo 1

O problema nos diz que dado um triângulo ABC qualquer, se ligarmos o ponto médio de AB ao ponto médio de AC, vamos obter um segmento MN paralelo ao terceiro lado (BC) e que vale a sua metade.

Para comprovar vamos ilustrar o enunciado.

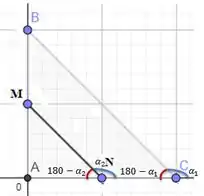
Como M é ponto médio de AB: AM = MB

Ou seja:

A B = 2 A M

Como N é ponto médio de AC: AN = NC

Ou seja:

A C = 2 A N

Se MN é paralelo a BC, então os ângulos entre as retas devem ser iguais:

α 1 = α 2

Passo 2

Então, precisamos calcular os ângulos, como são obtusos:

s e n   α = s e n   π - α = C a t e t o   O p o s t o H i p o t e n u s a

cos ⁡ α = - c o s   π - α = C a t e t o   A d j a c e n t e H i p o t e n u s a

Sendo assim:

t g   α = s e n   α cos ⁡ α = s e n   ( π - α ) - c o s   ( π - α )

Para α 1 :

s e n   π - α 1 = A B B C

c o s   π - α 1 = A C B C

Substituindo:

t g   α 1 = A B B C - A C B C = A B B C . - B C A C = - A B A C = - 2 A M 2 A N = - A M A N

Para α 2 :

s e n   π - α 2 = A M M N

c o s   π - α 2 = A N M N

Substituindo:

t g   α 2 = A M M N - A N M N = A M M N . - M N A N = - A M A N

Ou seja:

t g   α 1 = t g   α 2

  α 1 = α 2

Podemos concluir então que as retas MN e BC são paralelas.

Passo 3

A próxima etapa do problema é descobrirmos se M N = B C 2 .

Para isto, podemos observar que o triângulo AMN e ABC possuem os três ângulos iguais e então são semelhantes pelo caso AA (ângulo-ângulo). Então, se:

A B = 2 A M

A C = 2 A N

Por semelhança:

B C = 2 M N

Ou seja:

M N = B C 2

Concluindo que MN vale a metade do comprimento de BC.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4. A tabela a seguir dá a previsão de cinco dias de temperaturas máximas e mínimasem graus Celsius (°C). (a) Suponha que x e y denotem, respectivamente,as previsões de temperaturas máxima e mínima par
Encontre o domínio de f ∘ g para as funções f e g do exercício 47 .
Considere a família de funções y = x n , em que n é um inteiro. Os gráficos de y = x n são simétricos em relação ao eixo y se n for __________. Esses gráficos são simétricos em relação à origem se n f
Qual é o domínio natural de um polinômio?
Classifique cada equação como polinomial, racional, algébrica ou não uma função algébrica.(a) y = x + 2 (b) y = 3 x 4 - x + 1 (c) y = 5 x 3 + cos ⁡ 4 x (d) y = x 2 + 5 2 x - 7 (e) y = 3 x 2 + 4 x - 2