Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 78
Prove analiticamente que as três medianas de um triângulo encontram-se num ponto
Passo 1
O problema nos pede para provar que se traçarmos as três medianas do triângulo elas se encontrarão em um determinado ponto.
Para começar, precisamos saber que a mediana é um segmento de reta que liga um vértice do triângulo ao ponto médio do lado oposto. Ilustrando as mediatrizes para um triângulo qualquer ABC, temos:
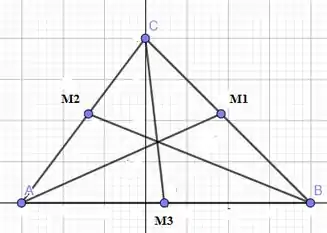
Dado que A(-b,0), B(a,0) e C(0,c), M1, M2 e M3 são pontos médios e podem ser calculados como a média dos pontos pertencentes a sua reta:
Agora podemos calcular seus pontos:
Com os pontos podemos obter a equação da reta para cada mediana.
Passo 2
Dada a equação geral da reta:
Para a mediana AM1:
Então:
Para a mediana BM2:
Então:
Igualando os valores de y:
Calculando y para AM1:
Calculando y para BM2:
Com isso nós comprovamos que as medianas AM1 e BM2 possuem um ponto em comum . O mesmo procedimento pode ser realizado para a mediana CM3 e o mesmo ponto em comum será obtido.
Resposta
Ei, a resposta está no passo a passo :)