Num triângulo, o ponto de intersecção das medianas, das alturas e o centro da circunferência circunscrita são colineares. Ache esses três pontos e comprove que eles são colineares no triângulo com vértices (2,8), (5,-1) e (6,6).
Passo 1
O enunciado do problema nos pede para traçar três pontos distintos: o de intersecção das medianas (G), intersecção das alturas (O) e o ponto que coincide com o centro da circunferência circunscrita ao triângulo (H). Uma vez descobertos os pontos G, O e H devemos provar que são colineares, ou seja, fazem parte de uma mesma reta.
Para começar vamos ilustrar o triângulo cujos vértices são A (2,8), B (5,-1) e C (6,6).
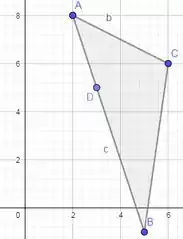
Obtido o triângulo precisamos obter os três pontos.
Passo 2
Para obter o ponto G, intersecção das medianas, precisamos saber que a mediana é um segmento de reta que liga um vértice do triângulo ao ponto médio do lado oposto:
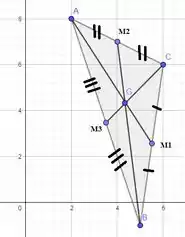
O ponto G também é chamado de baricentro e pode ser calculado como a média dos vértices, ou seja:
Então:
O segundo ponto, O, é o encontro das alturas do triângulo. As alturas ligam os vértices à linha suporte do lado oposto fazendo um ângulo de 90°. Como o triângulo é obtusângulo, um ângulo maior que 90° (C), as alturas de dois vértices são externas e, consequentemente, o ponto O. Sendo assim, devemos prolongar as retas suportes para que o ângulo reto seja atingido e as medianas possam ser desenhadas:
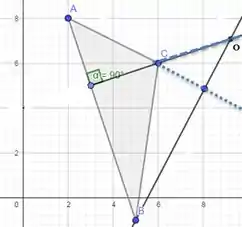
A intersecção das alturas é denominada ortocentro, e para achá-lo precisamos descobrir as inclinações de pelo menos duas retas suportes. Vou optar pelas retas AC e BC.
Reta AC: passa pelos pontos A (2,8) e C (6,6). Com os pontos e a equação geral da reta podemos descobrir a inclinação:
Substituindo:
Reta BC: passa pelos pontos B (5,-1) e C (6,6). Com os pontos e a equação geral da reta podemos descobrir a inclinação:
Substituindo:
Agora precisamos saber que para duas retas serem perpendiculares entre si, o coeficiente angular deve ser o oposto do inverso da outra. Como as alturas são perpendiculares às retas suportes podemos calcular sua inclinação.
Altura BO: é perpendicular a reta suporte AC:
Como a altura passa pelo ponto B a equação é:
Altura AO: é perpendicular a reta suporte BC:
Como a altura passa pelo ponto A a equação é:
Como o ponto é comum às duas alturas temos a certeza de que, para ele, os valores de y devem ser iguais:
Substituindo o x em qualquer equação:
Então:
O último ponto, H, o centro da circunferência circunscrita. Precisamos saber que a circunferência para ser circunscrita deve passar pelos três vértices do triângulo:
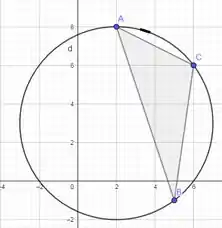
Para calcular as coordenadas do ponto H (), também chamado de circuncentro, devemos observar que os três pontos dados (A, B e C) estão à mesma distância do centro H. Isso porque a distância do centro até qualquer ponto da circunferência é igual ao raio.
Sabendo que a fórmula para a distância entre dois pontos é:
Então:
Onde:
Em :
Em :
Resolvendo:
Para x:
Então:
Descobertos os três pontos, precisamos saber se são colineares.
Passo 3
Para definir se são colineares podemos definir a inclinação da reta entre GO e OH. Como temos o ponto O comum às duas retas, se a inclinação for igual poderemos afirmar a colinearidade.
Sabendo que:
Para a reta GO:
Para a reta OH:
Sendo assim, os três pontos são colineares.
Resposta
Ei, a resposta está no passo a passo :)