Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 28
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Fazer o gráfico desse monstrinho seria uma sessão de tortura! Vamos tentar fatorar os polinômios e simplificar alguma coisa pra facilitar a nossa vida. Depois de simplificar, fazemos o gráfico e a partir do gráfico definimos o domínio e a imagem da função .
Passo 2
Vamos começar achando as raízes daquela função quadrática do denominador:
Por bhaskara:
Daí ficamos com:
E nossas duas raízes são:
E
E daí podemos reescrever o nosso polinômio assim:
Na nossa função original, ficamos com:
Passo 3
Vamos agora fatorar o Por bhaskara:
Daí:
E temos as nossas duas raízes:
E
E podemos reescrever a equação do 2º grau que tínhamos como:
Substituindo na nossa função
Já podemos dar uma simplificada!
Passo 4
Agora fatorando o outro polinômio do numerador do mesmo jeito:
Por bhaskara:
Daí:
Temos as nossas duas raízes da equação do 2º grau:
E
Fatorado com sucesso!
Agora substituindo na equação:
E podemos então simplificar de vez e nossa livrar dessa equação complicada e ficar somente com uma reta!
Passo 5
O gráfico vai ser o de uma reta com inclinação e fazendo vemos que o ponto pertence à reta. Ficamos com o gráfico:
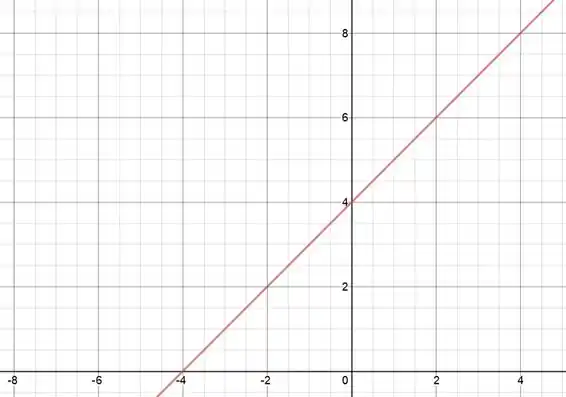
Passo 6
Uma reta está definida para qualquer valor de e também pode retornar qualquer valor em então tanto nosso domínio quanto a nossa imagem será . Ou seja:
Resposta
Domínio:
Imagem:
