Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 21
Um homem apara seu gramado toda quarta-feira à tarde. Esboce o gráfico da altura da grama como uma função do tempo no decorrer de um período de quatro semanas.
Passo 1
E aí pessoal, tudo tranquilo? Preparado pra fazer um exercício?
O enunciado diz que a grama é cortada toda quarta-feira. Essa grama vai crescer continuamente até a próxima quarta, quando ela vai ser cortada de novo, e aí ela vai crescer de novo... deu pra ver que o evento se repete né? E ele vai se repetir por quatro semanas.
A partir daí queremos obter o gráfico da altura da grama como uma função do tempo no decorrer de um período de quatro semanas.
Tem ideia de como fazemos isso? 👀
Passo 2
Isso que a gente tem é chamado de função peródica, ou seja, uma função que fica se repetindo indefinidamente.
No nosso gráfico, então, vai ter um desenho que fica se repetindo dentro do periodo que mandaram a gente desenhar (quatro semanas).
Dá uma olhada no jeitão do gráfico:
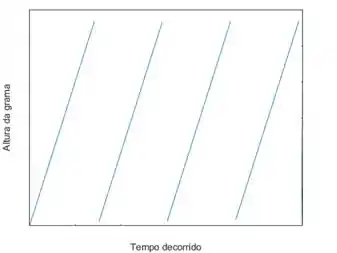
O menor ponto em cada uma dessas retas é quando a grama acabou de ser cortada (às quartas-feiras pela tarde). Ela cresce continuamente até a próxima quarta, atingindo sua altura máxima (logo antes da grama ser cortada). Feito o gráfico, acabou a questão!
Entendeu tudo? Responde Aí! 😇
Resposta
