Um avião vai de um aeroporto a outro em uma hora, e a distância entre eles é de . Se representa o tempo em minutos desde a partida do avião, seja a distância horizontal percorrida e a altura do avião.
a) Esboce um possível gráfico de .
b) Esboce um possível gráfico de .
c) Esboce um possível gráfico da velocidade no solo.
d) Esboce um possível gráfico da velocidade vertical.
Passo 1
Fala galera, beleza? Preparados para resolver essa questão sobre gráficos?

Seguinte... a questão nos diz que um avião voa de um aeroporto a outro (com km de distância entre eles) no intervalo de hora.
A questão nos dá ainda as seguintes informações:
- representa o tempo em minutos desde a partida do avião;
- representa a distância horizontal percorrida;
- representa a altura do avião.
A questão nos pede para esboçar alguns gráficos em função do tempo... que vamos mostrando à medida que formos respondendo cada letrinha, belezinha?
Aqui a gente vai utilizar muito a imaginação no sentido de analisar o movimento do avião em todo o percurso.
Então bora lá!! 😉
Passo 2
(a) O enunciado da questão nos diz que o gráfico de representa a distância horizontal do avião.
Se a gente pensar na decolagem dele, no início ele ta subindo, tentando ganhar altura.
Logo, inicialmente, a gente não vai ter uma variação de distância horizontal tão alta.
Logo em seguida, o avião vai ficar reto, paralelo com relação ao chão, depois de ganhar altura suficiente.
Ele vai fazer isso com uma velocidade constante, logo, a distância que ele percorre vai variar proporcionalmente ao tempo.
Ao final, a gente vai ter que pensar na aterrissagem: ele vai tentar perder altura e a distância horizontal vai variar bem pouco, até ele parar de vez.
Com isso, a gente já pode esboçar o nosso gráfico! Dá uma olhada:
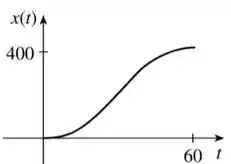
Deu pra sacar?
Resumindo: no inicio, varia pouco, depois varia de forma constante (que seria a parte que é reta do gráfico) e, por fim, volta a varia pouco até o avião parar.
Como o avião viaja por e com uma velocidade de , ele percorre .
No nosso gráfico, a distância está em quilômetros e o tempo em minutos.
Beleza? Bora pra próxima! 😊
Passo 3
(b) Aqui a gente tem que desenhar o gráfico da altura do avião, representada por .
A gente já fez essa aqui pela metade no passo passado, ficou faltando só desenhar o gráfico!
No item anterior, falamos que o avião inicialmente sobe, ganha altura e voa paralelo ao chão.
Depois disso, ele desce e a aterrissa.
Com isso, a gente já consegue esboçar o que a gente quer, dá uma olhada:
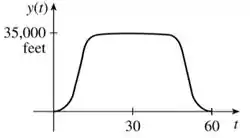
Deu pra sacar? No inicio e no final tem essa variação na altura mas, no resto do tempo, ela fica constante.
Se você estiver se perguntando o porquê desse , não te assusta!
É só que essa é a altura média que os aviões comerciais costumam voar, beleza?
Mas se você fez o gráfico sem essa informação, continua certinho!
Tranquilo até aqui? 😉
Passo 4
(c) Esse gráfico aqui é o de velocidade horizontal, ou seja, a velocidade com relação à .
No inicio, a velocidade vai aumentando (o avião ta parado e vai decolar, aí as turbinas são ligadas e ele vai andando devagar).
Esse aumento ocorre rapidinho, até o avião chegar à sua velocidade de .
Ele fica assim por um tempo e, depois, na hora de aterrissar, a velocidade dele vai diminuir.
No final das contas, o nosso gráfico vai ter um jeitão do gráfico da letra (c)! Dá uma olhada:
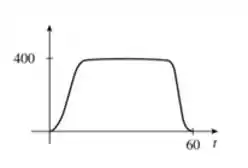
No eixo vertical temos a velocidade horizonatal em , enquanto no eixo horizontal temos o tempo em minutos.
A velocidade máxima que o avião atinge ta no comando da questão e é de .
Bacana, não é? 😐
Passo 5
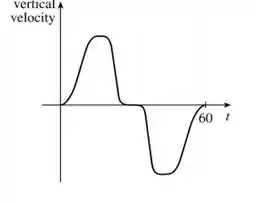
(d) Essa aqui é um pouco traiçoeira, então fica atento! Bora lá:
O avião começa a subir e a velocidade vertical dele vai aumentando, certo?
Depois, quando ele vai atingindo a altura suficiente que ele precisa, ele vai parando de subir e sua velocidade vai vertical vai se aproximando de zero.
Quando ele vai pousar, ele começa a ganhar velocidade na vertical novamente, até que ele vai aterrissar e sua velocidade na vertical vai se aproximando de zero de novo.
Beleza até aqui? Bora continuar então!
A gente tem que se atentar pra mais uma coisa: quando a gente vai fazer o gráfico de velocidade de qualquer objeto, a gente convenciona que, se o objeto se move em um sentido, a velocidade é positiva, enquanto que no sentido contrário é negativa.
E por que isso é importante?
Bom, uma hora o nosso avião sobe e outra hora ele desce, e a gente vai ter que fazer essa convenção.
Quando ele subir a gente vai convencionar que a velocidade é positiva e quando ele descer que ela é negativa, fechou?
Olha como fica o nosso gráfico:
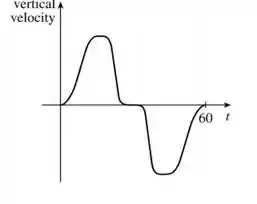
Na primeira metade é a etapa de subida (ele vai ganhando velocidade e, quando chega na altura desejada, vai perdendo até chegar em zero), enquanto a segunda a etapa de descida (que ta negativa por causa da convenção do sentido, não esquece!).
Entendeu direitinho?? Responde Aí! 😉
Resposta
a)
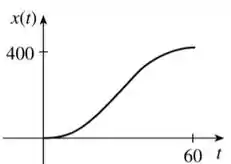
b)
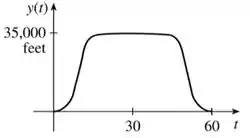
c)
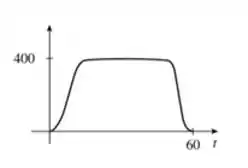
d)