Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.1 - Ex. 11

Determine uma equação da esfera com centro em ( 1 ,   - 4 ,   3 ) e raio 5. Qual é a intersecção dessa esfera com o plano xz?

Passo 1

Sabe aquela equação bem conhecida para a esfera?? Aquela x 2 + y 2 = 1 , essa equação é apenas para a coordenada ( x ,   y ) , e o valor 1 representa, basicamente, o raio dessa esfera, logo

x 2 + y 2 = r 2

O nosso problema nos dá as coordenadas no R 3 , o que fazemos?? Colocamos mais uma coordenada nessa equação de cima. Logo:

x 2 + y 2 + z 2 = r 2

Mas tem mais uma coisa nessa equação aí!! Ela só é válida para uma esfera cujo centro está na origem, ou seja, com centro em x ' = 0 ,   y ' = 0 ,   z ' = 0 .

E se o centro não está na origem, o que fazemos? Nesse caso, usamos a expressão abaixo:

x - x ' 2 + y - y ' 2 + ( z - z ' ) 2 = r 2

Se liga que o enunciado deu pra a gente as coordenadas do centro da nossa esfera, agora é só correr pro abraço!

Passo 2

Aplicando as coordenadas na equação que montamos,

x - 1 2 + y - ( - 4 ) 2 + ( z - 3 ) 2 = ( 5 ) 2

Organizando,

x - 1 2 + y + 4 2 + ( z - 3 ) 2 = 25

O problema nos pede a interseção com o plano x z , logo, y = 0 . Sendo assim, a nossa equação fica

x - 1 2 + 0 + 4 2 + ( z - 3 ) 2 = 25

x - 1 2 + 16 + ( z - 3 ) 2 = 25

x - 1 2 + ( z - 3 ) 2 = 25 - 1 6

x - 1 2 + ( z - 3 ) 2 = 9

Como, já havíamos dito que y = 0 , a equação da interseção da nossa esfera com o plano x z , será uma circunferência, centrada nos pontos x ' = 1 ,     z ' = 3   e o raio será R = 9 = 3 .

Repara que nós tínhamos uma equação de uma esfera no R 3 e a interseção dessa esfera em um plano será uma circunferência, que está no R 2 . Mais ou menos como no desenho abaixo.

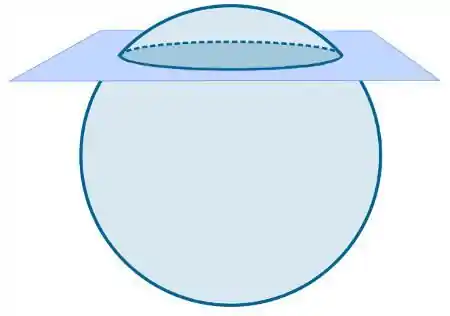
E terminamos!!

Resposta

A interseção da esfera com o plano será a circunferência de raio 3, centrada no ponto x ' = 1 ,   z ' = 3 .

Sua equação é dada por x - 1 2 + ( z - 3 ) 2 = 9 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6) Determne o vetor x → nas figuras:c)
Dados três pontos A,B e C não colineares, como na Figura 1.31, representar o vetor x → nos casos:a) x → = B A → + 2 B C →
Dados três pontos A,B e C não colineares, como na Figura 1.31, representar o vetor x → nos casos:b) x → = 2 C A → + 2 B A →
Dados três pontos A,B e C não colineares, como na Figura 1.31, representar o vetor x → nos casos:c) x → = 3 A B → - 2 B C →
Dados três pontos A,B e C não colineares, como na Figura 1.31, representar o vetor x → nos casos:d) x → = 1 2 A B → - 2 C B →