Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.3 - Ex. 4
Determine a equação da reta tangente ao gráfico de no ponto de abscissa . Esboce os gráficos de e da reta tangente.
Passo 1
Procuramos uma reta, então, procuramos uma equação do tipo:
Como queremos a reta tangente num ponto, seu coeficiente angular é a derivada da função neste ponto, ou seja,
Devemos então, encontrar :
Como temos, usando a regra de derivação, sabemos que
Se nesse caso , temos que:
Passo 2
Então,
Assim,
Basta agora achar o valor de , e como é o ponto de tangencia, ele também satisfaz a equação da reta:
Logo, a equação da reta tangente é:
Passo 3
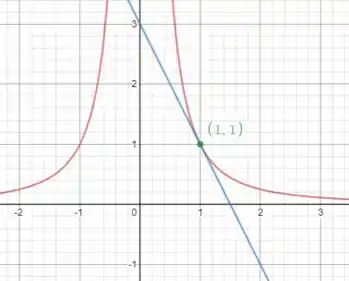
O gráfico de e sua reta tangente em então é:
Resposta
Exercícios de Livros Relacionados
Calcule g ' x sendo g dada por g x = x 100
Calcule g ' x sendo g dada por g x = x
Calcule g ' x sendo g dada por g x = x 4
Calcule g ' x sendo g dada por g x = 1 x
Seja r a reta que é tangente ao gráfico de f x = 1 x no ponto de abscissa p . Verifique que r intercepta o eixo x no ponto de abscissa 2 p .