Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.3 - Ex. 3

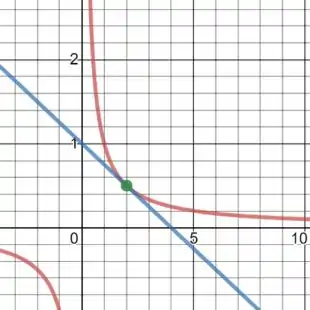
Determine a equação da reta tangente ao gráfico de f x = 1 x no ponto de abscissa 2 . Esboce os gráficos de f e da reta tangente.

Passo 1

Oi, galerinha! Tudo bom? Nesta questão temos que achar a equação da reta tangente. Para isso vamos usar a seguinte fórmula:

y - f x 0 = f ' x 0 x - x 0

Como problema diz que o ponto é na abcissa igual a 2 , temos que x 0 = 2 .

Então agora vamos achar f x 0 e f ' x 0 .

Passo 2

Vamos começar achando f x 0 . Como já vimos que x 0 = 2 :

f x 0 = 1 x 0 → f 2 = 1 2

Passo 3

Agora vamos encontrar f ' x .

Como

1 x = x - 1

temos, usando a regra de derivação, que

d d x x n = n x n - 1

Se nesse caso n = - 1 , temos que:

f ' x = - 1 x - 1 - 1 = - x - 2 = - 1 x 2

f ' x = - 1 x 2

Então,

f ' 2 = - 1 2 2 = - 1 4

Passo 4

Substituindo f x 0 e f ' x 0 na fórmula, ficamos com

y - 1 2 = - 1 4 x - 2

Logo, a equação da reta tangente é: y = - 1 4 x + 1

Passo 5

O gráfico de f e sua reta tangente em x = 2 então é:

Resposta

y = - 1 4 x + 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Derive a função. g u = 2 u+ 3 u
Derive a função.y = e^(x + 1) + 1
Derive a função. v = x + 1 x 3 2
Derive a função. y = a e v + b v + c v 2
São mostrados os gráficos da função velocidade de duas partículas, com t medido em segundos. Quando cada partícula está acelerando? Quando está freando? Explique