Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.6 - Ex. 29
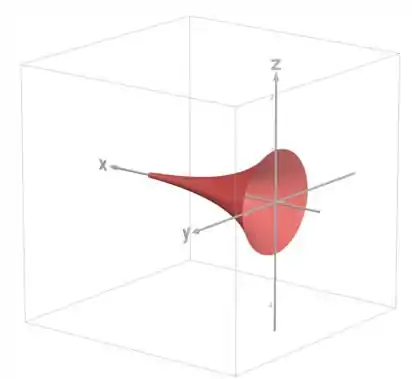
Determine as equações paramétricas da superfície obtida pela rotação da curva , , em torno do eixo e use-as para traçar o gráfico da superfície.
Passo 1
Faala, pessoal!
Essa questão pede pra gente encontrar a parametrização de uma superfície de revolução, e desenhar usando um software gráfico (no nosso caso, vai ser o Desmos).
Temos que lembrar que pra parametrizar uma superfície de revolução de uma curva em torno do eixo , fazemos:
Com , e os limites de definidos pela curva original .
Vamos começar definindo isso para a curva da nossa questão!
Depois, vamos usar o Desmos pra traçar o gráfico dessa superfície.
Passo 2
Nossa curva é
Então, a parametrização fica:
Com
E, como :
Passo 3
Para plotar esse gráfico no Desmos, vamos escrever no formato:
Então
Fica assim:
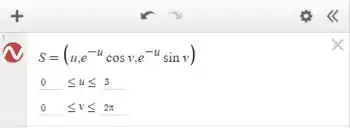
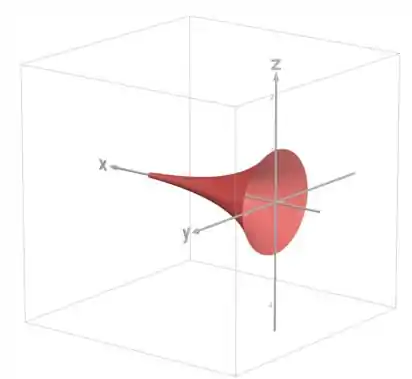
E o resultado:
Resposta
