Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 23

Determine uma representação paramétrica para a superfície.

A parte da esfera x 2 + y 2 + z 2 = 4 que está acima do cone z = x 2 + y 2

Passo 1

Fala, galera! =D

Nessa questão temos uma superfície com parte da esfera

x 2 + y 2 + z 2 = 4

Acima do cone

z = x 2 + y 2

E precisamos fazer uma representação paramétrica dessa superfície.

No gráfico abaixo podemos observar essa superfície:

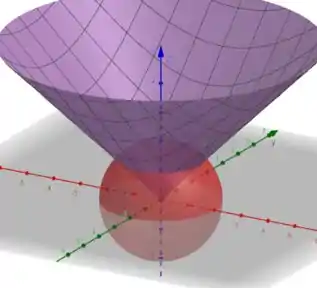
Passo 2

Primeiro vamos achar o ponto de interseção entre as duas figuras:

x 2 + y 2 + z 2 = 4

Como temos um cone z = x 2 + y 2 , então:

x 2 + y 2 + x 2 + y 2 2 = 4

Corta-se a raiz com o expoente quadrado:

x 2 + y 2 + x 2 + y 2 = 4

2 x 2 + 2 y 2 = 4

Dividindo todos os termos por 2 :

x 2 + y 2 = 2

O que nos dá:

z = x 2 + y 2 = 2

Passo 3

Vamos agora isolar o z da esfera, e vamos pegar a parte positiva, pois queremos a parte acima do cone, agora definido por

z = 2

Assim,

x 2 + y 2 + z 2 = 4

Isolando z , teremos

z = 4 - y 2 - x 2

Se deixarmos x e y serem os parâmetros, as equações paramétricas são:

x = x               y = y             z = 4 - y 2 - x 2

Com

x 2 + y 2 ≤ 2

Resposta

x = x               y = y             z = 4 - y 2 - x 2 , com x 2 + y 2 ≤ 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Case as equações com os gráficos identificados po I - V I e dê razões para sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. r u , v = ucos ⁡ v i + u s
Use um sistema algébrico computacional para produzir um gráfico que se pareça com o que está dado.
Use um sistema algébrico computacional para produzir um gráfico que se pareça com o que está dado.
Case as equações com os gráficos identificados po I - V I e dê razões para sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. x = u - sen ⁡ u cos ⁡ v ,
Case as equações com os gráficos identificados po I - V I e dê razões para sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. r u , v = cos ⁡ v i + sin