Se e , determine . Esboce , e como vetores com início na origem.
Passo 1
Nesse exercício devemos calcular o produto vetorial de dois vetores e depois desenhar eles no espaço. Vemos da questão anterior que qualquer que seja o vetor e o produto vetorial entre eles será ortogonal à ambos os vetores.
Temos que:, agora vamos calcular o produto vetorial:
Passo 2
Depois de achar o produto vetorial nós temos que esboçar os vetores , e .
Já temos às coordenadas dos vetores acima que são:
, e
logo basta traçar o vetor partindo da origem até às coordenadas de cada um deles.
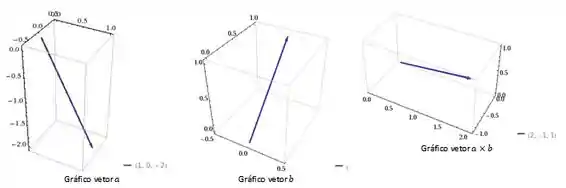
Resposta
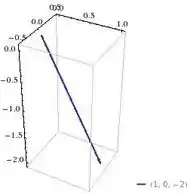
Gráfico vetor
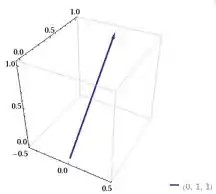
Gráfico vetor
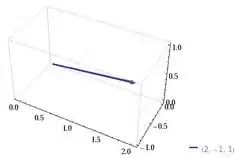
Gráfico vetor