Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 12
Determine e faça o esboço do domínio da função.
Passo 1
E aí, galera! Tudo bem?
Bom, aqui nessa questão nós queremos determinar o domínio de . Em outras palavras, queremos saber quais valores de e podem ser usados para que seja real.
Para definir o domínio é melhor olharmos para as restrições.
Além disso, vamos fazer também o esboço da região no plano que representa o domínio dessa função.
Tranquilo? Vem comigo então.
Passo 2
Para determinar o domínio devemos nos perguntar: quais valores de e podemos usar para calcular ?
Se a função é definida como
nós sabemos que e devem ser números maiores ou iguais a zero. Do contrário, a função assumirá valores complexos, o que não desejamos.
Podemos escrever isso de forma mais matemática, isto é, dizemos que o domínio de será a região onde e .
Portanto,
e
Passo 3
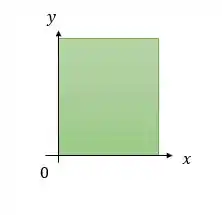
A região no plano onde e é o primeiro quadrante. Assim, o domínio é o primeiro quadrante desse plano.
Veja na figura abaixo:
Resposta
e