Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 18
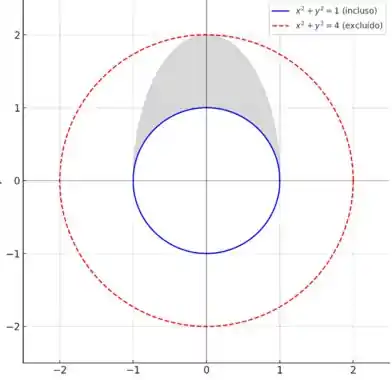
Determine e faça o esboço do domínio da função.
Passo 1
Fala ai, tudo certinho?
Patriu resolver um exercícios?
Para resolver o problema vamos primeiro determinar o domínio da função , verificar a expressão dentro da raiz quadrada e o argumento do logaritmo. Podemos comparar as duas condições para encontrar o domínio, que é a região entre as curvas. E finalizamos fazendo um esboço no plano cartesiano para visualizar a região válida.
O gráfico nos ajudará a entender melhor onde a função é definida.
Mãos a OBRA!
Passo 2
Queremos determinar o domínio de . Ou seja, queremos saber que valores de , que podem ser usados para que seja real.
Para definir o domínio é melhor olharmos para as restrições.
Note que temos duas indeterminações:
A primeira se dá por conta da raiz, então sabemos que
Ou até mesmo
Com raio igual a 1
Passo 3
E a segunda é por causa do ln, então sabemos que
Ou até mesmo
Com raio igual a 2
Assim, o domínio de é
Passo 4
O domínio da função será a interseção dessas duas regiões:
- A região fora ou sobre o círculo de raio 1.
- A região dentro do círculo de raio 2.
Portanto, o domínio da função é o anel entre os círculos de raios 1 e 2, excluindo o círculo de raio 2.
