Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.1 - Ex. 67

Nos Exercícios 65-68, encontre e esboce o domínio de f . Em seguida, encontre uma equação para a curva de nível ou superfície da função passando pelo ponto dado.

f x ,   y = ∫ x y d θ 1 - θ 2 ,       0 ,   1

Passo 1

Uma função f de duas variáveis é uma regra que associa a cada par ordenado de números reais x ,   y de um conjunto D um único valor real, denotado por f x ,   y . O conjunto D é o domínio de f e sua imagem é o conjunto de valores possíveis de f , ou seja:

f x ,   y | ( x ,   y ) ∈ D

No enunciado temos a seguinte função:

f x ,   y = ∫ x y d θ 1 - θ 2

Pela regra da integral, sabemos que:

∫ d u a 2 - u 2 = u a  

Resolvendo nossa integral:

∫ x y d θ 1 - θ 2 = θ   x y =   y   - x  

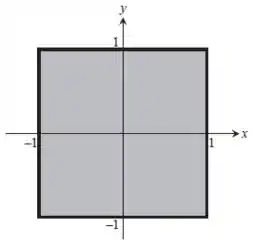
Sendo assim, podemos escrever o domínio da nossa função da seguinte maneira:

D = x ,   y ∈ R 2 | - 1 ≤ x ≤ 1   e - 1 ≤ y ≤ 1

Logo, conseguimos obter a Figura:

Passo 2

O conjunto de pontos no plano onde uma função f x ,   y possui um valor constante f x ,   y = c é denominado curva de nível de f .

Substituindo o valor de x e y na equação:

y   - x   = 1   - ( 0 )  

Então nossa curva de nível é:

y   - x   = π 2

Resposta

D = x ,   y ∈ R 2 | - 1 ≤ x ≤ 1   e - 1 ≤ y ≤ 1 ) ;

Curva de nível 🡪 y   - x   = π 2   .

Exercícios de Livros Relacionados

Desenhe a curva de nível da função mostrando vários níveis. f x , y = l n ⁡ ( x 2 + 4 y 2 )
Combine a função com seu gráfico (rotulado I-VI). Dê razões para suas escolhas. f x , y = 1 1 + x 2 + y 2 f x , y = 1 1 + x 2 y 2 f x , y = ln ⁡ x 2 + y 2 f x , y = cos ⁡ x 2 + y 2 f x , y = x y f x ,
Esboce o gráfico da função. f x , y = 2 - x 2 - y 2
Encontre e esboce o domínio da função. f x , y = x 2 + y 2 - 4
Encontre e esboce o domínio da função.g (x , y) = (x - y)/(x + y)