Nos Exercícios 53-60, esboce uma superfície de nível típica para a função.
Passo 1
Oi galerinha, tudo bem com vocês? Vamos fazer esse exercício juntos?! Então, vem comigo!
No plano, os pontos onde uma função de duas variáveis independentes tem um valor constante formam uma curva no domínio da função. No espaço, os pontos onde uma função de três variáveis independentes tem um valor constante formam uma superfície no domínio da função.
O conjunto de pontos no espaço onde uma função de três variáveis independentes tem um valor constante é chamado superfície de nível de .
No nosso exercício, temos a seguinte equação:
O valor de é a distância entre a origem e o ponto .
As superfícies de níveis são , onde , é uma esfera de raio centrada na origem. A superfície de nível consiste somente na origem. Então quando varia sobre uma das esferas com centro , o valor de permanece fixo, formando uma família de esferas concêntricas com raio .
Passo 2
Então, para esboçar uma superfície de nível típica para esta função, vamos considerar :
Representada pela Figura:
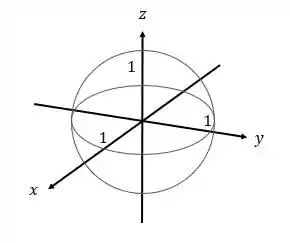
Tchau galerinha.
Resposta
Resposta no Passo 2.