Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.4 - Ex. 6

Determine a velocidade, a aceleração e a rapidez da partícula cuja função posição é dada. Esquematize o caminho da partícula e desenhe os vetores velocidade e aceleração para os valores de t especificados.

r → t = s e n t   i → + 2 c o s t   j → ,     t = π 6

Passo 1

Fala ai galerinha!

Tudo tranquilo? Essa é uma questão bem prática, digo isso porque temos que derivar a posição para encontrar a velocidade, e derivar a velocidade para encontrar a aceleração. Viu!?

Na questão também pede o desenho dos vetores velocidade e da aceleração da partícula, neste caso teremos que pedir ajuda a um software.

Agora é só resolver!

Passo 2

Vamos começar o problema resolvendo a derivada da posição, cuja função posição é dada por r t = s e n   t   i + 2 cos ⁡ t   j . Depois, vamos analisar as propriedades para t = π 6 .

Função posição:

r t = s e n   t   i + 2 cos ⁡ t j

A velocidade será a derivada da posição em relação ao tempo.

v t = d r t d t

v t = d d t ( s e n   t   i + 2 cos ⁡ t j )

v t = d d t ( s e n   t )   i + d d t ( 2 cos ⁡ t ) j

Resolvendo individualmente d d t s e n   t = cos ⁡ t e d d t c o s   t = - s e n   t

v t = c o s   t   i - 2 sen ⁡ t j

Passo 3

A aceleração será a derivada da posição em relação ao tempo.

a t = d v t d t

a t = d d t ( cos ⁡ t   i - 2 sen ⁡ t j )

a t = d d t c o s   t i - d d t ( 2 sen ⁡ t ) j

Resolvendo individualmente d d t c o s   t = - sen ⁡ t e d d t 2   s e n   t = - cos ⁡ t

a t = - s e n   t   i → - 2 cos ⁡ t   j →

Passo 4

A rapidez é o módulo do vetor velocidade:

v t = cos ⁡ t 2 + - 2 s e n   t 2

v t = c o s 2 t - 4 s e n ² t

Passo 5

Vamos agora substituir t = π 6   na função da posição, velocidade e aceleração.

- Posição em t = π 6

r t = s e n   t   i + 2 cos ⁡ t j

r t = s e n   π 6   i + 2 cos ⁡ π 6 j

r t = 1 2   i + 2 . 3 2 j

r t = 1 2   i + 3 j

Passo 6

- Velocidade em t = π 6

v t = c o s   t   i - 2 sen ⁡ t j

v t = c o s   π 6   i - 2 sen ⁡ π 6 j

v t = 3 2 i - 2     . 1 2 j

v t = 3 2 i - j

Passo 7

- Aceleração em t = π 6

a t = - s e n   t   i → - 2 cos ⁡ t   j →

a t = - s e n   π 6   i → - 2 cos ⁡ π 6   j →

a t = - 1 2   i → - 2 3 2   j →

a t = - 1 2   i → - 3   j →

Passo 8

A rapidez para t = π 6 ,   será:

v t = c o s 2 t - 4 s e n 2 t

v t = c o s 2 π 6 - 4 s e n 2 π 6

v t = 3 2 2 - 4   - 1 2

v t = 3 4 - 4  

v t = 7 4  

v t = 7 2

Passo 9

Para esquematizar o caminho da partícula e desenhar os vetores velocidade e aceleração, vamos analisar!

- A trajetória é determinada pela função posição r ( t ) = ( s i n ( t ) , 2 c o s ( t ) ) . Essa trajetória é uma curva no plano x y .

Ponto em t = π 6 ​: O ponto 1 2 , 3   no plano.

- Vetor Velocidade em t = π 6 ​ : O vetor v   6 π ​ = 3 2 i - j é um vetor que aponta na direção ( 3 2 , - 1 ) .

- Vetor Aceleração em t = 6 π ​: O vetor a π 6 = - 1 2 i - 3 j é um vetor que aponta na direção ( - 1 2 , - 3 ) .

Passo 10

Hora de esboçar o gráfico! Mas antes se liga na analise dos vetores!

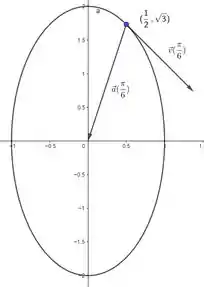
Resposta

Os vetores velocidade e aceleração no ponto dado são:

v → π 6 = 3 2   i → -   j →

a → π 6 = - 1 2   i → - 3   j →

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se uma partícula com massa m se move com vetor posição r t , então seu momento angular é definido como L t = mr t × v t e seu torque é definido como τ t = mr t × a t . Mostre que L ' t = τ t . Deduza
Um foguete que queima o combustível carregado dentro de si enquanto se move no espaço tem, no instante t , velocidade v t e massa m t . Se os gases provenientes da combustão escapam a uma velocidade d
A função posição de uma nave espacial é r t = 3 + ti + 2 + ln ⁡ tj + 7 - 4 t 2 + 1 k e as coordenadas de uma estação espacial são 6 ,4 ,9 . O capitão quer que a nave ataque na estação espacial. Quando
A tabela fornece coordenadas de uma partícula movendo-se no espaço ao longo de uma curva lisa. Determine a velocidade média nos intervalos de tempo 0 ; 1 ,0,5 ; 1 , 1 ; 2e1 ; 1,5 . Estime a velocidade
A figura mostra a trajetória de uma partícula que se move com vetor posição r → ( t ) no instante t .Desenhe um vetor que represente a velocidade média da partícula no intervalo de tempo 2 ≤ t ≤ 2,4 .