Determine se a função dada é biunívoca. Faça um esboço do gráfico da função.
Passo 1
A questão pede para verificarmos se a função é biunívoca, isto é, se ela é injetora. Para que uma função seja inteira, diferentes valores de devem dar, necessariamente, em diferentes valores de . Assim, devemos ter
Derivando , obtemos , de modo que é crescente. Sendo assim, diferentes valores de acarretam necessariamente diferentes valores de , de modo que a função é biunívoca. Formalmente, se tomarmos e reais com , chegaremos em , cuja única solução real é . Assim, a única forma de ser igual a é se e forem o mesmo número. Provamos assim que é injetora!
Passo 2
O gráfico de é dado a seguir:
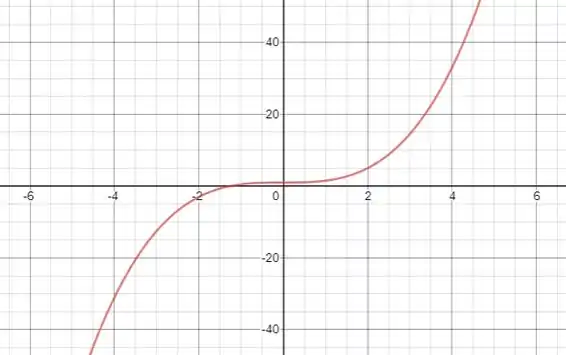
Observe que o gráfico satisfaz o teste da reta horizontal!
Resposta
É biunívoca.