Determine se a função dada é diferenciável em um valor , sendo que está definida por fórmulas diferentes em lados diferentes de . Para isso, pode ser usado o resultado seguinte, que é uma consequência do Teorema do Valor Médio. Teorema: Seja uma função contínua em e suponha que exista . Então é diferenciável em e .

Mostre que:

é contínua em Determine se é diferenciável em . Se for, encontre o valor da derivada nesse ponto.

Calculando o limite:

Onde:

Vamos olhar para os limites laterais e eles devem coincidir.

Limite lateral pela esquerda:

Limite lateral pela direita:

Opa, os limites laterais coincidiram, então:

Para a função ser contínua em :

Como vimos:

Agora, olhando para a função:

Quando , a função vale obedece essa equação: . Então:

Muito bom! Dessa forma, é contínua em , já que:

Agora, vamos olhar para o teorema do enunciado:

“Teorema: Seja uma função contínua em e suponha que exista . Então é diferenciável em e .”

Para saber se é diferenciável em , falta só que verificar se existe, pois já vimos que é contínua em .

Vamos calcular o limite:

Se , então:

Calculando os limites laterais:

Limite lateral pela esquerda:

Limite lateral pela direita:

Como os limites laterais coincidiram, o limite existe e:

Como vimos que é contínua em e existe, então é diferenciável em e, portanto:

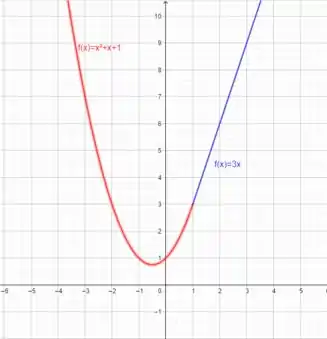
Falta só esboçar o gráfico. Olhando para a função, de novo:

Vemos que até o ponto , essa função é uma parábola com concavidade voltada para cima e deslocada para esquerda, cortando o eixo em e não cortando o eixo .

Depois de , a função passa a ser uma reta .

Nosso gráfico fica assim ó:

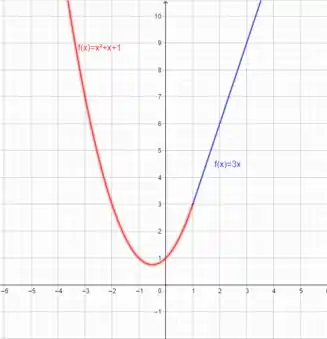
Agora, sim, acabou o problema!