Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 73

Se f ( x ) = l n x e g ( x ) = 4 - x^2 , determine as funções f @ g , g @ f , f @ f , g @ g e seus domínios.

Passo 1

Então, galera, vamos lembrar algumas coisinhas:

  1. f @ g é a mesma coisa que f ( g ( x ) ) , ou seja, onde tem x , em f , você joga g ( x ) . E assim vale pra quaisquer letras que você colocar, desde que elas sejam funções.
  2. O domínio de uma função são todos os valores possíveis pra x , ok?

Agora, partiu pro Passo 2!

Passo 2

Vamos fazer a f @ g .

f ( x ) = l n x e g ( x ) = 4 - x^2

( f @ g ) ( x ) = f ( g ( x ) ) = l n ( 4 - x^2 ) -> ( f @ g ) ( x ) = l n ( 4 - x^2 )

Pra achar o domínio, precisamos saber se:

O que tá dentro pode ser qualquer positivo? Pode, pois existe l n de número positivo.

Pode ser qualquer negativo? Não, pois não existe l n de número negativo.

Pode ser 0? Não, pois não existe l n de 0.

Então, 4 - x^2 > 0 . Olha só o gráfico dessa parábola:

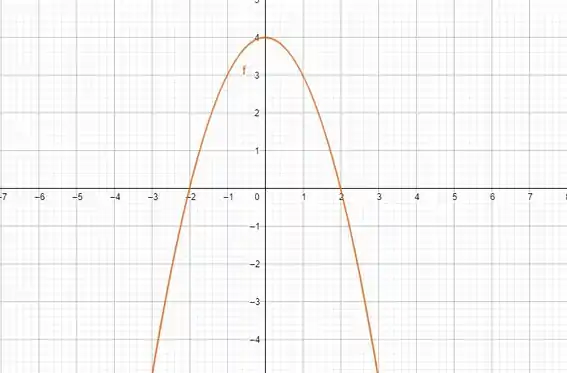
A gente tem que ver onde 4 - x^2 > 0 , que é no intervalo [-2,2].

Então:

D ( f @ g ) = [ - 2,2 ]

Passo 3

Vamos fazer a g @ f .

f ( x ) = l n x e g ( x ) = 4 - x^2

( g @ f ) ( x ) = g ( f ( x ) ) = 4 - ( l n x )^2 -> ( g @ f ) ( x ) = 4 - ( l n x )^2

Pra achar o domínio, precisamos saber se:

O que tá dentro do logaritmo pode ser qualquer positivo? Pode, pois existe l n de número positivo.

Pode ser qualquer negativo? Não, pois não existe l n de número negativo.

Pode ser 0? Não, pois não existe l n de 0.

Então, x > 0 .

D ( g @ f ) = ( 0 , + oo )

Passo 4

Vamos fazer a f @ f .

f ( x ) = l n x

( f @ f ) ( x ) = f ( f ( x ) ) = l n ( l n x )

Pra achar o domínio, precisamos saber se:

O que tá dentro do logaritmo pode ser qualquer positivo? Pode, pois existe l n de número positivo.

Pode ser qualquer negativo? Não, pois não existe l n de número negativo.

Pode ser 0? Não, pois não existe l n de 0.

Então, l n x > 0 . E onde ele é positivo? Do 1 em diante, sem ser o próprio 1.

Então:

D ( f @ f ) = ( 1 , + oo )

Passo 5

Vamos fazer a g @ g .

g ( x ) = 4 - x^2

( g @ g ) ( x ) = g ( g ( x ) ) = 4 - ( 4 - x^2 )^2 = 4 - ( 16 - 8 x^2 + x^4 ) = 4 - 16 + 8 x^2 - x^4 = - x^4 + 8 x^2 - 12

Pra achar o domínio, precisamos saber se:

O que tá dentro pode ser qualquer positivo? Pode.

Pode ser qualquer negativo? Pode.

Pode ser 0? Pode.

Então, x pode ser qualquer real.

D ( g @ g ) = R

Resposta

D ( f @ g ) = [ - 2,2 ]

D ( g @ f ) = ( 0 , + oo )

D ( f @ f ) = ( 1 , + oo )

D ( g @ g ) = R

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use os gráficos das funções f e g na figura ao lado para resolver os seguintes problemas.Encontre f ( - 2 ) e g ( 3 ) .Com quais valores de x temos f x = g x ? Com quais valores de x temos que f x2 ?
19. Em cada parte descreva a família de curvas.(x - a)^2 + (y - a)^2 = 1^2 . y = a + ( x - 2 a ) ² ²
20. Encontre uma equação para uma parábola que passe pelos pontos 2 ,0 ,( 8 ,18 ) e - 8 ,18 .
18.Escreva uma equação para o gráfico obtido refletindo o gráfico de y = x - 1 , pelo eixo y, então distendendo-o verticalmente por um fator de 2, depois transladando-o para baixo 3 unidade e, por fim
25. Dê condições sob as quais duas funções, f e g , serão inversas, e dê vários exemplos dessas funções.Descrea a relação entre os gráfico de y = f ( x ) e y = g ( x ) quando f e g são funções inversa