Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 47
Dados e , faça os gráficos de e juntos. Em seguida, descreva como a aplicação da função valor absoluto em afeta o gráfico de .
Passo 1
Olá, gente! Vamos lembrar uma coisa antes de começarmos a questão: “função valor absoluto” nada mais é do que a função módulo, ok? Bom, aqui ele quer que você faça o gráfico das duas juntas e mostre o que mudou quando você inseriu aquele módulo ali em relação a . Ok? Vamos lá!
Passo 2
Olha só o gráfico das duas juntas:
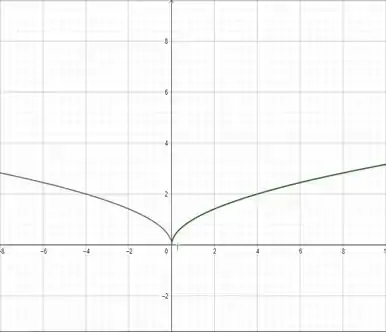
O que mudou colocando o módulo? A verde () é aquela parte da direita e a cinza () é a parte da esquerda e a parte da direita também (tá debaixo da verde). A diferença é que a acrescentou a parte da esquerda, em relação a , que é o reflexo da parte direita em um “espelho” em cima do eixo . Além disso, o domínio passou de pra , porque a função módulo vai tirar os sinais, então não importa se o for negativo.
Resposta
A diferença é que a aplicação da função módulo acrescentou o “reflexo” da função no lado esquerdo do gráfico e o domínio passou de pra .