Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.Revisão - Ex. 2
Use os gráficos das funções e na figura ao lado para resolver os seguintes problemas.
- Encontre e .
- Com quais valores de temos
- Com quais valores de temos que
- Quais são o dominio e imagem de
- Encontre os zeros de e .
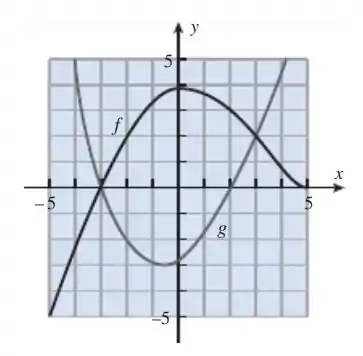
Passo 1
Blezinha galera, na letra (a), queremos encontrar e dado o gráfico:
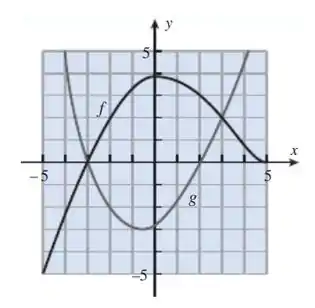
E observando o gráfico, vemos que esses pontos são:
Portanto:
Passo 2
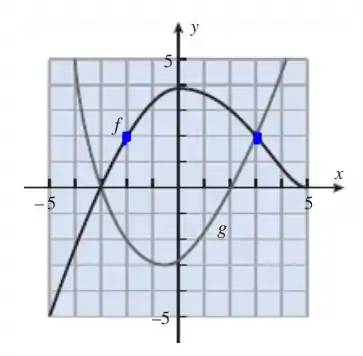
Na letra (b), queremos os pontos onde , esses pontos são os conhecidos pontos de interseção, ou seja, onde as curvas se cruzam, que são esse pontinhos aqui:
E podemos ver que isso ocorre, em e .
Passo 3
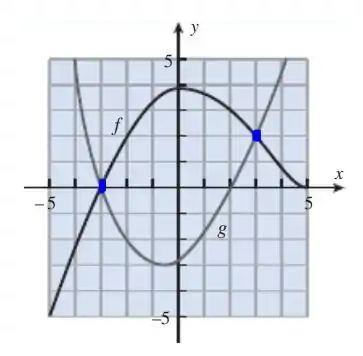
E agora na letra (c), queremos descobrir os valores de que fazem com que , ou seja, se traçarmos uma reta em , temos:
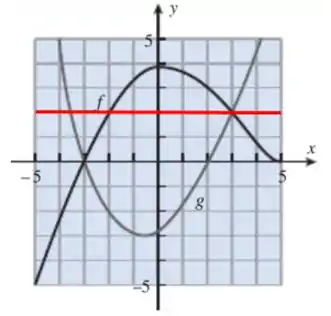
Logo para e para , temos que .
Passo 4
O dominio de vai de até e sua imagem vai de -5 até 4:
E para , temos:
Resposta
- .
- e .
- Para e para , temos que .
- .
- .
Exercícios de Livros Relacionados
(a) Esboce o gráfico de y = a x com a = ± 1 , ± 2 , ± 3 em um único sistema de coordenadas.(b) Esboce o gráfico de y = x + b com b = ± 1 , ± 2 , ± 3 em um único sistema de coordenadas.(c) Esboce algun
Esboce o gráfico da equação fazendo as transformações apropriadas no gráfico de uma função potência básica. Confira seu trabalho com um recurso gráfico.(a) y = 2 x + 1 2 (b) y = - 3 x - 2 3 (c) y = -
Esboce o gráfico da equação fazendo as transformações apropriadas no gráfico de uma função potência básica. Confira seu trabalho com um recurso gráfico.(a) y = 1 - x + 2 (b) y = 1 - x + 2 3 (c) y = 5
Esboce o gráfico de y = x 2 + 2 x completando o quadrado e fazendo as transformações apropriadas no gráfico de y = x 2 .
(a) Use o gráfico de y = x para ajudar a esboçar o gráfico de y = x .(b) Use o gráfico de x 3 para ajudar a esboçar o gráfico de y = x 3 .