Enunciado

Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 12.4 - Ex. 36

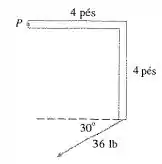
Determine a intensidade do torque em se for aplicada uma força de 36 lb, como mostrado.

Passo 1

O torque de uma força é dado pelo produto vetorial de um vetor distância pela força de aplicação. Portanto,

O vetor distância é a distância entre o ponto P até o ponto de aplicação da força. Utilizando a geometria do nosso problema, se assumirmos que o ponto P tem coordenadas e o ponto (o eixo é positivo para direita e o eixo positivo para cima), temos o seguinte vetor :

Agora que determinamos o vetor , só nos basta decompor a força . Utilizando também a geometria do problema, temos:

Passo 2

Pronto, agora que conseguimos determinar cada um desses vetores, podemos fazer o produto vetorial entre eles para obter o vetor torque! Portanto,

Agora que obtivemos o vetor torque, vamos calcular o seu módulo. Ele é dado por:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam ∧ e ∧ * os produtos vetoriais associados às duas orientações distintas de V 3 . Exprima: a → ∧ * b → em função de a → ∧ b → ; a → ∧ * b → ∧ * c → em função de a → ∧ b → ∧ c → ; a → ∧ * b → ∧ * c

No triângulo A B C , A H é a altura relativa ao vértice A . Prove que B C → ∧ ( A B → ∧ A C → ) é paralelo a A H .

São dados os pontos O , A , B e C .(a) Prove que o vetor x → A B C = O A → ∧ O B → + O B → ∧ O C → + O C → ∧ O A → não depende do ponto O , isto é, qualquer que seja o ponto P , P A → ∧ P B → + P B →

O vetor v → é ortogonal aos vetores u → = 2 ,- 1 ,3 e w → = 1 ,0 ,- 2 e forma ângulo agudo com o vetor j → . Calcular v → , sabendo que v → = 3 6

Dados os vetores u → = 2 ,- 1 ,1 ,v → = ( 1 ,- 1 ,0 ) e w → = ( - 1 ,2 ,2 ) , calcular:c) ( u → + v → ) × ( u → - v → )