Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 11.Exercício - Ex. 33
São dados os pontos , , e .
(a) Prove que o vetor não depende do ponto , isto é, qualquer que seja o ponto , (isto justifica a notação ).
(b) Exprima o vetor em função de , , .
(c) Prove que , e são colineares se, e somente se, .
(d) Suponha que , e não são colineares. Obtenha um vetor ortogonal ao plano determinado por esses pontos, em função de .
Passo 1
Vamos começar “abrindo” um pouco esses termos que aparecem no produto vetorial:
Dê uma olhada no primeiro termo, por exemplo:
Vamos fazer um desenho para entender o que isso significa:
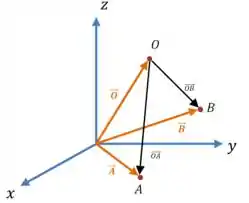
Ou seja, aplicando a propriedade distributiva:
Fazendo isso para os outros termos:
Todo produto vetorial de um vetor por ele próprio é zero! Então vai sumir em todos os termos:
Agora olha o que acontece quando a gente soma tudo:
Para finalizar, lembre que o produto vetorial é anticomutativo, ou seja:
Fazendo essas trocas de sinal dentro daqueles parênteses:
Então todos os termos entre parênteses vão se anular:
Ou seja, o não depende do ponto !
Passo 2
(b) Vamos dar uma olhada na expressão do enunciado:
Usando a mesma técnica de antes:
Ou seja:
Aplicando a propriedade distributiva:
Lembrando que o produto vetorial de vetores iguais é nulo, vamos sumir com aquele :
E usando mais uma vez essa propriedade aqui:
Ficamos com:
Que é exatamente a expressão que a gente encontrou lá em cima para o ! Ou seja:
Então para escrever em termos de , , é só copiar a fórmula do item (a) substituindo , e :
Resolvido!
Passo 3
(c) Agora queremos provar que , e são colineares se, e somente se, .
Vamos pensar o seguinte, se três pontos são colineares, então existe alguma reta que passa pelos três, certo? No desenho isso fica assim:
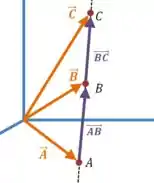
O que acontece com nesse caso?
Bom, se os pontos são colineares, então e são paralelos. Outra forma de dizer isso é afirmando que o ângulo entre eles é zero.
Nesse caso o módulo do produto vetorial é:
Como , ficamos com:
E então:
E podemos fazer o caminho contrário sem problemas. Ou seja, se , então necessariamente e formam um ângulo que mede zero, e por isso os pontos são colineares.
Passo 4
(d) Por último queremos encontrar um vetor ortogonal ao plano formado por , e em função de .
Primeiro vamos entender melhor quem é esse plano! Uma forma de defini-lo (pelo menos sua direção) é usando dois vetores distintos que envolvam , e .
Mas dê uma olhada na nossa fórmula para :
Ela envolve justamente os vetores que dão o plano contendo , e . O produto vetorial de dois vetores sempre te dá um terceiro vetor perpendicular aos outros dois!
Isso quer dizer que é um vetor perpendicular ao plano formado por , e .
Então o vetor ortogonal que estamos procurando é qualquer múltiplo de :
Onde é um número qualquer.
Resposta
(a) Demonstração.
(b)
(c) Demonstração.
(d) Qualquer múltiplo de é ortogonal ao plano formado por e .