Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 9.4 - Ex. 8

O bistmuto-210 tem uma meia-vida de cinco dias.

a) Se uma amostra tem massa de 800   m g , encontre uma fórmula para a massa que restará depois de t dias.

b) Calcule a massa depois de 30 dias.

c) Quando a massa será reduzida para 1   m g ?

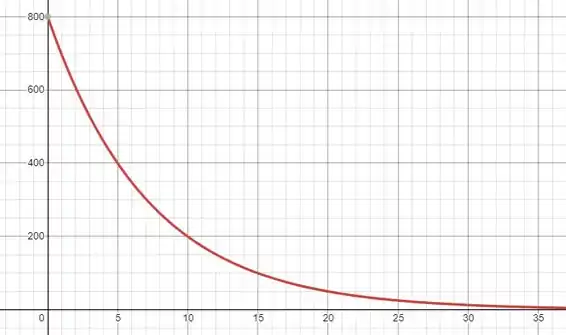
d) Esboce o gráfico da função massa.

Passo 1

Esse é um problema sobre decaimento radioativo! Sabemos que o decaimento radioativo é exponencial, do tipo

m t = m 0 e - k t

Já temos a massa inicial m 0 = 800 :

m t = 800   e - k t

Foi dado o tempo de meia-vida que representa o tempo para que a amostra caia pela metade. Assim, temos que

m 5 = m 0 2 = 800 2 = 400

Portanto,

400 = 800   e - 5 k

Logo,

e - 5 k = 1 2 ⇒ e 5 k = 2 ⇒ 5 k = ln ⁡ 2 ⇒ k = ln ⁡ 2 5 ≈ 0,139

Portanto,

m t = 800   e - 0,139 t

Passo 2

Após 30 dias, a massa será

m 30 = 800   e - 0,139   ⋅   30 = 800   e - 4,17

Assim,

m 30 = 12,3   m g

Passo 3

Para achar o tempo no qual a massa é 1   m g , fazemos

m t = 1 ⇒ 800 e - 0,139 t = 1 ⇒ e 0,139 t = 800

Logo,

0,139   t = ln ⁡ 800

Portanto,

t = 48,1   d i a s

A seguir fazemos um esboço de m ( t ) :

Resposta

m t = 800   e - 0,139 t

m 30 = 12,3   m g

t = 48,1   d i a s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 1 a 32,resolva a equação diferencial. Se for dada uma condição inicia,l encontre,também, a solução que satisfaz. d y d t = 3 - 6 t + y - 2 t y
Em cada um dos problemas de 1 a 32,resolva a equação diferencial. Se for dada uma condição inicia,l encontre,também, a solução que satisfaz. d y d t = 1 + c o s t 2 - s e n y
x y ' = y + x e y / x
d y d x = x 2 - 1 y 2 + 1 , y - 1 = 1
e x + 1 d y d x = y - y e x