Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.3 - Ex. 28

  1. Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescente
  2. Identifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem

g x = x 4 - 4 x 3 + 4 x 2

Passo 1

Primeiramente, necessitamos calcular a derivada d f para encontrar os pontos críticos

g ' x = 4 x 3 - 12 x 2 + 8 x

Igualamos a zero

4 x 3 - 12 x 2 + 8 x = 0

4 x   x - 2 x - 1 = 0

x = 0   ,   x = 1   e   x = 2

Pontos críticos : 0,1 , 2

Passo 2

Agora, vamos fazer o estudo do sinal para verificar onde a função cresce e decresce. Beleza?

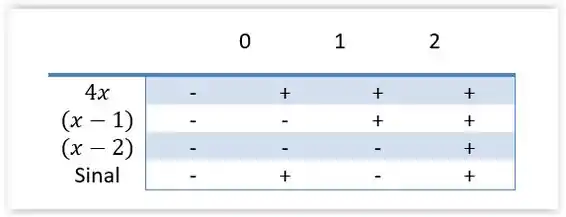
Logo,

g   é crescente nos intervalos 0,1 ⋃   ( 2 ,   ∞ )

g é decrescente nos intervalos - ∞ , 0 ⋃ ( 1,2 )

Passo 3

Assim, temos que o valores mínimos locais de g 0 = 0 no ponto x = 0 e g 2 = 0   em x = 2 , o valor máximo local em g ( 1 ) = 1 no ponto x = 1 . Não há máximo absoluto e o ponto de mínimo absoluto é 0 em x =   0   o u   x = 2 -

Resposta

  1. g   é crescente nos intervalos 0,1 ⋃ 2 ,   ∞ ;   g é decrescente nos intervalos - ∞ , 0 ⋃ ( 1,2 )
  2. Mínimos locais de g 0 = 0 no ponto x = 0 e g 2 = 0   em x = 2

Máximo local em g ( 1 ) = 1 no ponto x = 1 .

Não há máximo absoluto e o ponto de mínimo absoluto é 0 em x =   0   o u   x = 2 -

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os valores extremos (absoluto e local) das funções e onde ocorrem: y =3 + 2 x - x 2
Determine os valores extremos (absoluto e local) das funções e onde ocorrem: y = x + 1 x 2 + 2 x + 2
Determine os valores extremos (absoluto e local) das funções e onde ocorrem: y = x x 2 + 1
Determine os valores extremos (absoluto e local) das funções e onde ocorrem: y = cos - 1 ⁡ ( x ² ) ²
Determine os pontos críticos,extremidades de domínio e valores extremos (absolutos e locais) da função: y = x 2 3 ( x + 2 )