Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.6 - Ex. 37a
37. a) Determine a inversa de . Faça o gráfico de junto de sua inversa. Adicione a reta ao seu esquema, tracejada ou pontilhada para contrastar.
Passo 1
Para fazermos a inversa da função, assim como discutido na seção 6 do George, devemos escrever uma função , isto é, isolar a variável na função (supondo que seja a variável) e em seguida trocarmos as variáveis para escrevermos a inversa na forma convencional, que é , tranquilo? Se liga!
Passo 2
Escrevendo , temos:
Agora trocando as variáveis para o formato convencional:
Passo 3
Agora que temos a inversa, plotando os gráficos, teremos:
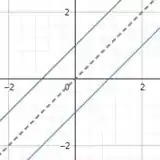
No qual a reta azul é , a verde é e a pontilhada é .
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 53 e 54, resolva em k .54. a)e 5 k = 1 4
Determine se a função composta f ∘ g é par ou ímpar em cada um dos seguintes casos: f e g são ambas pares.
Se f e g forem duas funções tal que f ∘ g x = x e g ∘ f x , então f e g serão funções inversas. Mostre que f e g são funções inversas f x = 1 x + 1 g x = 1 - x x
Determine se a função composta f ∘ g é par ou ímpar em cada um dos seguintes casos: f é par e g é ímpar.
Determine se a função composta f ∘ g é par ou ímpar em cada um dos seguintes casos: f é ímpar e g é par.