Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 3
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos pede para determinar uma janela retangular apropriada para a função dada e usá-la para fazer o gráfico da função:
Mas que janela é essa??
Então... quando a gente olha um gráfico, a gente quer tirar todas as informações que estão contidas nele. E, para isso, o gráfico não pode estar nem grande demais para o plano cartesiano e nem pequeno demais.
O tamanho ideal é aquele que contém o máximo de informações possíveis que podemos extrair do gráfico. Para isso, precisamos calcular pontos chaves que nos dirão o tamanho correto da janela.
Como nesse caso, é uma parábola de concavidade para cima (porque o coeficiente de é positivo), uma janela retangular apropriada precisaria incluir seu ponto de mínimo e suas raízes.
Esse ponto de mínimo vai estar localizado no vértice dessa par��bola e para calculá-lo nós podemos usar a fórmula do vértice:
para encontrar a coordenada desse ponto e depois substituir esse valor em para obter a coordenada . Lembrando que a forma geral de uma parábola é:
Então, no nosso caso, , e .
E para encontrar as raízes dessa equação, vamos usar a fórmula de Bháskara:
Vamos lá!
Passo 2
Vamos escolher nossa janela analisando o ponto de mínimo, então vamos começar calculando o vértice da parábola usando a fórmula que vimos no passo anterior:
Então, a coordenada do ponto mínimo é . Nós precisamos agora da coordenada , então vamos substituir esse valor na função:
Portanto, nosso ponto de mínimo é:
Passo 3
Agora vamos calcular as raízes da equação usando a fórmula de Bháskara:
Fatorando a raiz e simplificando, obtemos:
Então, nossas raízes são:
E
Passo 4
Como precisamos de uma janela que nos dê uma visão mais completa, vamos usar para um valor de a . E para o intervalo de a .
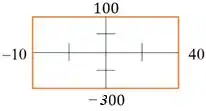
Agora com o gráfico, temos:
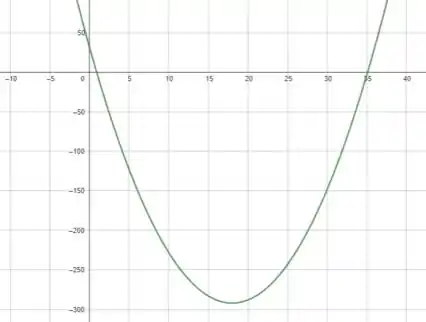
Valeu, galera! Até a próxima! 😉