Faça o gráfico da função:
Comece pelo gráfico de uma das funções padrão apresentadas nas figuras 1.14-1.17 e aplique a mudança adequada.
Passo 1
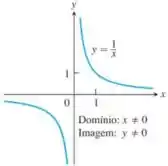
De acordo com as funções apresentadas na seção 1.1 do George, temos que a função que mais se assemelha com a que temos é a seguinte:
Cujo gráfico é:
Passo 2
Agora que sabemos a função que mais se assemelha com a que temos, vamos ir inserindo as informações da função dada pela questão na função padrão que estamos utilizando como base, tudo bem?
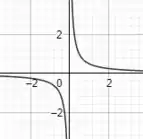
Primeiramente, o que significa esse multiplicando na função? Quando há um fator multiplicativo desse tipo, isso significa que a função está sendo comprimida verticalmente. Sendo assim, a função apresenta o seguinte gráfico:
Passo 3
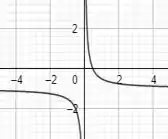
Por fim, para chegarmos na função que nos foi dada pela questão basta subtrairmos 1 unidade na função, não é? Sempre que há uma subtração na função o gráfico dessa função é deslocado para baixo. Como a subtração é de apenas 1 unidade, então o gráfico da função vai ser deslocado de 1 unidade para baixo. Fazendo isso, já teremos a nossa função final, que é:
Cujo gráfico é o seguinte:
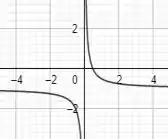
Resposta
O gráfico de é: