Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.4 - Ex. 16

Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função

y = tan ⁡ 25 x

Passo 1

Fala aí, galerinha!

Nesse problema foi dada uma função

y = tan ⁡ 25 x

E nosso objetivo é determinar uma janela retangular apropriada para esboçar o gráfico dessa função...

Tem ideia de como fazemos isso?

A questão quer que a gente determine um intervalo em x e y que proporcione uma visualização adequada da função que foi dada.

Pra isso temos que analisar que função é essa e ter uma ideia de como ela se comporta...

Se escolhermos uma janela pequena, nosso gráfico não terá muitos detalhes e pode acabar distorcendo a interpretação que temos sobre ele.

Se a janela for muito grande vai parecer que estamos olhando para uma formiga a 100 m de distância, que tambem pode distorcer a interpretação que temos sobre a função.

Veja só!

Passo 2

Nesse caso temos a função

y = tan ⁡ 25 x

Sabemos que a função tan ⁡ x é uma função periódica cujo periodo é π , ou seja, a cada x = π a função se repete.

Mas temos uma pequena mudança... o conteúdo dentro da tangente é 25 x , então o periodo desse gráfico será 25 vezes menor... ou seja, π 25 .

Dessa forma, se quisermos esboçar n períodos desse gráfico, fazemos

∆ x = n T

Onde T é o período.

Digamos que queremos esboçar 3 repetições do gráfico ( 3 períodos), então fazemos

∆ x = 3 · π 25 ≅ 0,4

Como x assume valores negativos e positivos, o intervalo em x da nossa janela será

x = - ∆ x 2 ; ∆ x 2

Portanto...

x = - 0,4 2 ; 0,4 2

x = - 0,2 ; 0,2

Tranquilo até aqui?

Passo 3

A função tangente é uma função de tende ao infinito no final de um período, então o intervalo em y para a nossa janela não pode ser um número tão baixo pois não vamos conseguir observar essa tendência.

Particularmente podemos escolher qualquer número entre 10 e 40 para ∆ y .

Nesse caso vamos escolher

∆ y = 20

Assim como ∆ x , vamos definir nosso intervalo em y da nossa janela como

y = - ∆ y 2 ; ∆ y 2

Justamente devido a simetria da função.

Substituindo

y = - 20 2 ; 20 2

y = - 10 ; 10

E finalmente, nossa janela terá as seguintes coordenadas

x = - 0,2 ; 0,2 y = - 10 ; 10

Esboçando o gráfico da função y = tan ⁡ 25 x a partir das características que descrevemos durante o problema, chegamos em

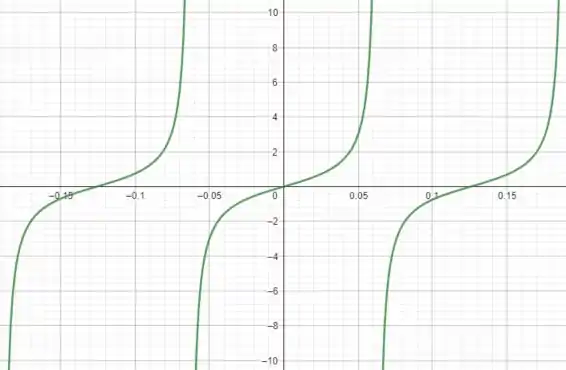
E aí! o que achou? Responde Aí!

Resposta

x = - 0,2 ; 0,2 y = - 10 ; 10

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre todas as soluções da equação, com duas casas decimais de precisão. x 4 - x = 1
Encontre todas as soluções da equação, com duas casas decimais de precisão. x = x 3 - 1
Faça o gráfico da função f x = x 2 30 - x em uma janela apropriada. Por que parte do gráfico parece faltar?
Faça o gráfico da função usando quantas visualizações retangulares você precisar para descrever a verdadeira natureza da função. f x = 1 - cos ⁡ x 4 x 8
Vimos, no exemplo 9, que a equação cos ⁡ x = x tem exatamente uma solução. a) Use um gráfico para mostrar que a equação cos ⁡ x = 0,3 x tem três soluções e encontre-as com duas casas decimais de preci