Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.11 - Ex. 11
Verifique a aproximação linear dada em . Então determine os valores de para os quais a aproximação linear é precisa dentro de 0,1.
Passo 1
Se queremos linearizar uma função , fazendo uma aproximação tendo como base um valor , aplicamos a seguinte fórmula:
Queremos aproximar , e podemos fazer isso tomando como base , como mostra o enunciado. Nossa aproximação fica então:
Passo 2
Primeiro calculamos . Temos:
Agora devemos ter o valor da derivada da função para . Derivando:
Então, para :
Colocando na fórmula:
Passo 3
Agora queremos saber para quais valores de a aproximação linear é precisa dentro de 0,1. Isso significa que queremos que a diferença entre e seja menor que 0,1:
Somando na inequação:
Isso significa que se deslocarmos o gráfico de de 0,1 para cima e para baixo, o gráfico de deve estar dentro dessa faixa. Podemos fazer isso montando os gráficos de , e , e vendo para quais valores de isso ocorre:
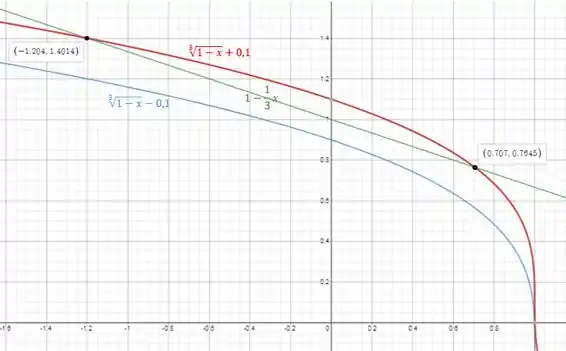
Podemos ver que o intervalo para essa precisão é: