Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.4 - Ex. 13
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função
Passo 1
E aí pessoal?
Aqui nessa questão temos que definir a janela adequada e fazer o gráfico da função:
Mas o que é janela apropriada?
Bom, o gráfico vai mostrar um intervalo da função e nós temos que escolher de onde até onde vamos mostrar.
A janela apropriada é um intervalo que mostre suficiente pra gente entender o comportamento da função, mas que não seja grande demais pra ela não ficar apertadinha. Na prática, deve mostrar pontos importantes da função (máximos, mínimos, raízes, assíntotas e etc).
Bom a gente já sabe algumas coisas das funções trigonométricas. O domínio são todos os reais, porque não tem restrição pros valores de . Sendo um cosseno, também sabemos que ele vai ser periódico, então precisamos de um intervalo que mostre os períodos e sua amplitude.
Então vamos começar calculando o domínio da função, as raízes e outros pontos que precisam aparecer na nossa janela!
Passo 2
Outra coisa que sabemos é que a função cosseno é limitada entre e para . Então não tem porque a janela ser muito maior que esse intervalo.
E pra achar o seu período, vamos igualar o argumento a
Então período vai ser:
Queremos mostrar uns 2 períodos, pra dar pra entender esse comportamento periódico. Mas não tem necessidade de mostrar muitos.
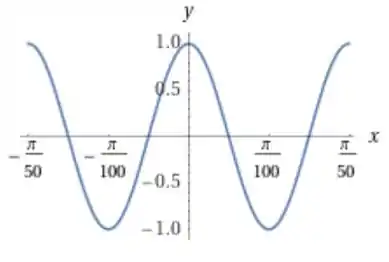
Então uma janela adequada pode ser:
Repara só no que acontece se usamos um intervalo muito maior: o gráfico fica desnecessariamente repetitivo. Então essa janela abaixo já não é tão adequada.
