Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.3 - Ex. 7
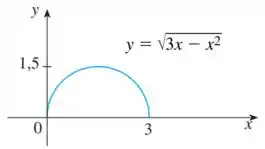
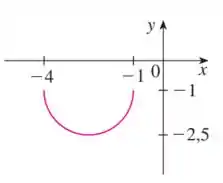
O gráfico é dado. Use transformações para criar a função cujo gráfico é mostrado.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos deu o gráfico da função e pediu pra gente usar transformações para criar a função cujo o gráfico é dado abaixo:
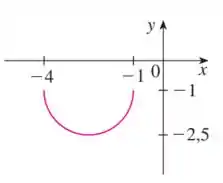
Pra isso, a gente precisa lembrar que os deslocamentos verticais e horizontais, assim como as expansões e reflexões, da curva no gráfico seguem algumas regrinhas. Olha só:
Sendo assim, vamos analisar o gráfico da função que ele nos deu e verificar quais deslocamentos podem ter modificado a curva para ficar no formato do segundo gráfico dado e a partir daí, definir a nossa nova função.
Vamos lá!
Passo 2
O enunciado nos deu o gráfico de :
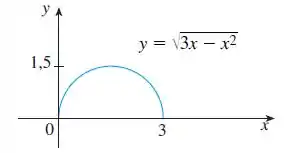
Então, vamos compará-lo com o segundo gráfico:
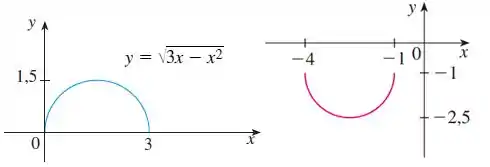
Observe que ocorreu uma reflexão em torno do eixo , porque a curva estava com a concavidade voltada para baixo e passou a ficar com a concavidade para cima! Quando isso acontece, segundo as regrinhas que vimos no passo , multiplicamos a função por . Assim, temos:
Agora observe também que o gráfico caminhou unidades para a esquerda, então houve um deslocamento. Dessa forma, nós precisamos somar a o mesmo fator de deslocamento, nesse caso, somamos ao argumento da função. Ou seja:
Por fim, repare que o gráfico andou uma unidade para baixo, então eu tenho que diminuir essa unidade da equação. Assim, ficamos com:
E chegamos na nossa nova função.
Valeu, galera! Até a próxima! 😉