Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.3 - Ex. 15

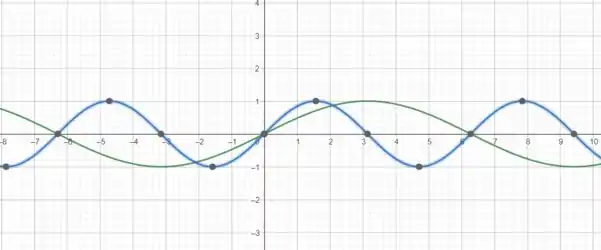
Faça o gráfico da função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção 1.2 e então aplicando as transformações apropriadas.

y = s e n x 2

Passo 1

E aí! tudo certinho? 😁

Para resolver essa questão, primeiro precisamos entender as transformações aplicadas à função seno básica y = sin ⁡ x para obter a função y = sin ⁡ x 2

função seno básica, y = sin ⁡ x , tem um período de 2   π , onde x varia de + - ∞ .

Ela atinge seus máximos em k π + π 2 , 1 e seus mínimos em k π - π 2 , - 1 , onde k é um número inteiro.

A função y = sin ⁡ x 2 é uma função seno que foi comprimida horizontalmente por um fator de 2. Isso significa que o período da função será 2 × 2 π = 4 π .

Além disso, os máximos e mínimos serão alcançados em metade dos lugares, comparado com a função básica. Portanto, os máximos ocorrem em k π + π 2 , 1 e os mínimos em k π - π 2 , - 1 , onde k é um número inteiro.

Passo 2

Agora, para fazer o gráfico da função y = sin ⁡ x 2 sem marcar pontos, começamos com o gráfico da função y = sin ⁡ ( x )   e aplicamos as transformações apropriadas:

1. O período é aumentado para 4 π

2. Os máximos ocorrem em k π + π 4 , 1 e os mínimos em k π - π 4 , - 1

A função seno básica y = sin ⁡ ( x ) tem a seguinte forma:

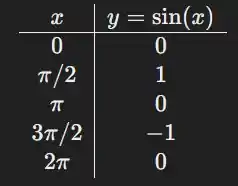
Passo 3

Agora, para y = sin ⁡ x 2 vamos aplicar as transformações:

1. O período é 4 π , então os valores de x serão multiplicados por 2.

2. Os máximos ocorrem em k π + π 4 , 1 e os mínimos em k π - π 4 , - 1

Portanto, o gráfico de y = s i n x 2 seria similar ao gráfico de   y = s i n ( x ) , mas comprimido horizontalmente por um fator de 2 e os pontos máximos e mínimos ajustados conforme mencionado na explicação.

Fazendo isso, obtemos:

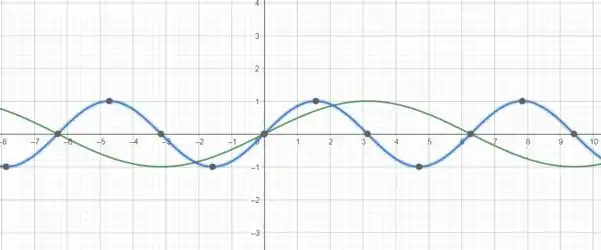
Entendeu tudo? Responde Aí! 😎

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Antropologistas usam um modelo linear que relaciona altura do fêmur humano com sua altura. O modelo permite a um antropologista determinar a altura de um individuo quando apenas parte do esqueleto (in
Faça o gráfico da função a mão, não usando pontos, mas a partir dos gráficos de uma das funções padrão dadas na seção 1.2, e então aplique as transformações apropriadas.y = 1 - 1 x
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção 1.2, e então aplicando as transformações apropriadas.y = - x 2
Faça o gráfico da função à mão, não usando pontos, mas a partir dos gráficos de uma das funções padrão dadas na seção 1.2, e então aplique as transformações apropriadas.y = 3 - 2 c o s x
Faça o gráfico da função à mão, não usando pontos, mas a partir dos gráficos de uma das funções padrão dadas na seção 1.2, e então aplique as transformações apropriadas.y = 2 x + 1