Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.3 - Ex. 6
O gráfico de é dado. Use transformações para criar a função cujo gráfico é mostrado.
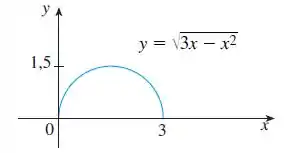
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
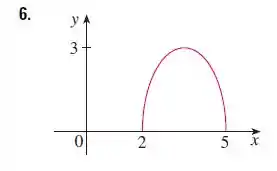
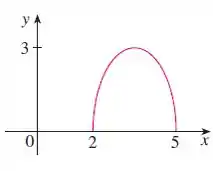
O enunciado nos deu o gráfico da função e pediu pra gente usar transformações para criar a função cujo o gráfico é dado abaixo:
Pra isso, a gente precisa lembrar que os deslocamentos verticais e horizontais, assim como as expansões e reflexões, da curva no gráfico seguem algumas regrinhas. Olha só:
Sendo assim, vamos analisar o gráfico da função que ele nos deu e verificar quais deslocamentos podem ter modificado a curva para ficar no formato do segundo gráfico dado e a partir daí, definir a nossa nova função.
Vamos lá!
Passo 2
O enunciado nos deu o gráfico de :
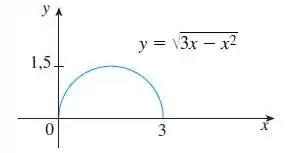
Então, vamos compará-lo com o segundo gráfico:
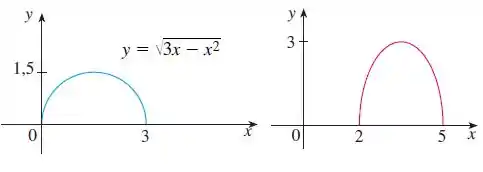
Observe que a curva andou unidades para a direita no eixo . Quando isso acontece, de acordo com as regrinhas que vimos no passo , subtraímos unidades ao que está dentro da função, ou seja, dentro do argumento. Então, ficamos com:
Mas não é só isso, o gráfico também foi alterado na vertical. Observe que ele dobrou de altura, saindo de para , no eixo .
Isso significa que ele sofreu uma expansão vertical por um fator de unidades e, segundo as regrinhas do passo , isso quer dizer que a função vai ser multiplicada por esse fator, ou seja:
Passo 3
Beleza, já sabemos quais foram as transformações que a nossa curva sofreu, agora vamos a função que a define. Pra isso, vamos substituir na função e multiplicar ela por dois. Fica assim:
E multiplicando por dois, temos a nova função:
Valeu, galera! Até a próxima! 😉