Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 28

Faça o gráfico dos polinômios P x = 3 x 5 - 5 x 3 + 2 x e Q x = 3 x 5 na mesma tela, usando primeiro a janela retangular [ - 2 ,   2 ] por [ - 2 ,   2 ] e então mudando para [ - 10 ,   10 ] por [ - 10000 ,   10000 ] . O que você pode observar a partir desses gráficos?

Passo 1

O problema fornece dois polinômios

P x = 3 x 5 - 5 x 3 + 2 x

E

Q x = 3 x 5

E ele pede para plotarmos seus gráficos em janelas diferentes. Mas porquê isso? A ideia é entender que na mudança de janelas, ou seja, onde a gente vê a curva, vemos um pedaço, ou todo, do comportamento da função.

No caso de polinômios, dependendo da janela, não veremos nem se ele tem raízes! Então por isso a importância da janela adequada!

Ah, mais uma coisa: temos dois polinômios em que o termo líder (termo de maior potência) são iguais. Isso significa que nos infinitos ( + ∞ e - ∞ ) os comportamentos das funções será igual! Mudando apenas o comportamento no “meio”. Isso significa mudança nas raízes!

Beleza? Bora começar?

Passo 2

A primeira janela é [ - 2 ,   2 ] por [ - 2 ,   2 ] :

Plotando os dois polinômios

Q x = 3 x 5 ( a z u l )

P x = 3 x 5 - 5 x 3 + 2 x ( r o s a )

Temos:

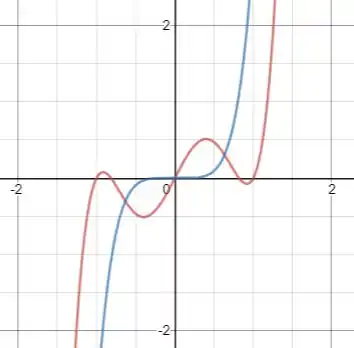
Note que os comportamentos nos infinitos são iguais

P x → + ∞ = + ∞ ; Q x → + ∞ = + ∞

P x → - ∞ = - ∞ ; Q x → - ∞ = - ∞

O que muda é que a curva P ( x ) (em rosa) cruza o eixo x 5 vezes! Ou seja, temos 5 raizes! Embora a curva Q cruze apenas uma, a raiz em x = 0 é de multiplicidade 5 !

Tranquilo? Bora mudar a janela?

Passo 3

A segunda janela é [ - 10 ,   10 ] por [ - 10000 ,   10000 ] :

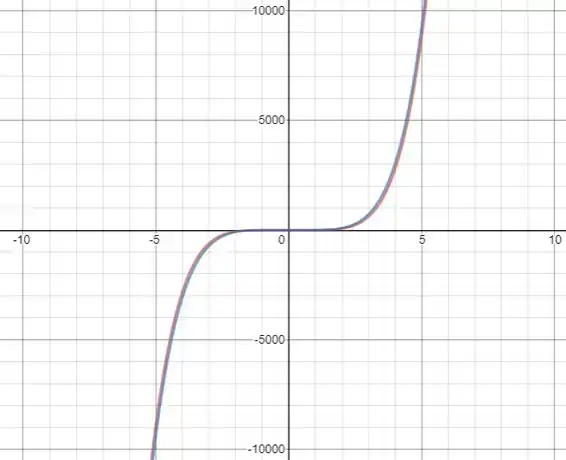
Note que agora estamos olhando as funções de bem mais longe, assim aquelas raízes da função rosa nem são perceptíveis! Isso porque o termo líder das duas é igual e quando nos afastamos estamos vendo seu comportamento líder!

E o que podemos concluir com isso?

Passo 4

Vemos que na primeira janela é possível ver os detalhes da função, enquanto na segunda, observando de “longe” as duas funções parecem ser iguais, por causa da igualdade do termo líder. Todavia, quando damos um zoom, vemos que elas tem um comportamento diferente para - 2 ≤ x ≤ 2 , e aí o comportamento “do meio” fica mais evidente!

Beleza? Espero ter ajudado!

Resposta

Esboço de gráfico. Quando as funções tem o mesmo termo líder, com uma janela grande vemos o comportamento dele. Quando diminuímos a janela, as diferenças ficam mais evidentes.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que f seja uma função par, g seja uma função ímpar e tanto f como g sejam definidas na reta real ℝ. Quais das seguintes funções (quando definidas) são pares? E ímpares? e )g 2 = g g
Faça o gráfico da função: y = | x^2 - 1 |
Uma função pode ser tanto par quanto ímpar? Justifique sua resposta.
Suponha que f seja uma função par, g seja uma função ímpar e tanto f como g sejam definidas na reta real ℝ. Quais das seguintes funções (quando definidas) são pares? E ímpares? d )f 2 = f f
Faça o gráfico da função: y = ( - 2 x ) 2 3 Comece pelo gráfico de uma das funções padrão apresentadas nas figuras 1.14-1.17 e aplique a mudança adequada.