Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 31
Determine o limite infinito.
Passo 1
Bom galera, esse enunciado é meio esquisitinho! O negócio é que ele já nos diz que o limite é infinito, então não é isso que queremos focar em discutir.
O nosso objetivo aqui é entender o sinal desse resultado, se vai ser infinito positivo ou negativo.
E pra isso, precisamos reparar nesse sinalzinho de + que aparece na nossa expressão
Isso é uma nomenclatura de limites laterais. Significa que estamos considerando que tende a 5 somente por um lado. No caso, como o sinal é de positivo, estamos nos aproximando de pela direita, ou seja, por valores maiores que 5.
(se a gente tivesse um sinal de – seriam valores menores que 5)
Agora vamos calcular o resultado considerando isso que relembramos!
Passo 2
Lembrando que o limite de uma razão é igual a razão dos limites:
No numerador, isso de limite lateral não vai fazer diferença, porque seja o resultado inifinitesimalmente maior ou menor que 6, o sinal vai ser positivo nos dois casos:
Mas no denominador vai fazer diferença, porque o resultado vai ser 0. Mas quando estamos falando de limite, não bem 0 e sim algo MUUUUIIIIITOOOO pertinho de zero. E aí faz diferença se estamos chegando da direita ou da esquerda, porque muda o sinal do resultado.
No caso, como estamos nos aproximando pela direita, estamos falando de valores maiores que 5, então o limite a seguir vai ser um número que é QUASE zero, mas positivo.
E aí a gente usa essa nomenclatura de , só pra indicar que é “um zero positivo”. Esquisito falar em sinal de zero, eu sei, mas lembre-se que no limite, estamos apenas TENDENDO a zero!
Passo 3
Retornando pra cá:
Encontramos que:
E aí que está o pulo do gato!
A gente já ta cansado de saber que se dividimos um número finito por zero (NOS LIMITES), a gente acha infinito.
Mas temos que lembrar que dividindo um número positivo por outro positivo, temos um resultado positivo!
Então nosso infinito aqui vai ser positivo.
Uhuuulll finalmente!
Passo 4
Podemos confirmar o valor obtido no passo 1 através da análise do gráfico da função:
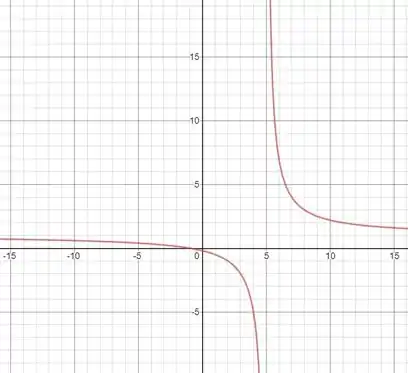
Viu, chegando pela direita, temos um limite pro infinito POSITIVO!