Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.2 - Ex. 32
Determine o limite infinito.
Passo 1
Fala aí! tudo certinho?
Nesse problema temos que mostrar que o limite
Tende a infinito.
Tem ideia de como fazemos isso?
Nesse caso, nossa função do limite é uma função logarítmica
Portanto não temos muitas simplificações que podemos fazer para resolver esse problema...
Mas essa família de funções possui algumas características interessantes e podemos usá-las para obter o resultado.
Veja só!
Passo 2
Nesse caso, tende a pela direita, ou seja, tende a valores infinitesimalmente maiores que .
Nós já vimos como é o comportamento da função , mas se não lembra, vamos refrescar a memória...
A função tende a quando se aproxima de , a função não está definida para , em , e em , .
Dessa forma, podemos expressar o gráfico da função como.
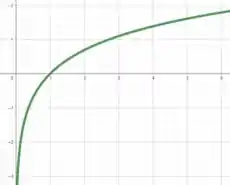
Mas você pode estar se perguntando: “como isso vai me ajudar?”
Nós respondemos: vamos analisar o comportamento do conteúdo do e verificar o que acontece no gráfico de ...
Bacana?
Passo 3
No limite, tende a mas sempre maior que .
Isso significa que o conteúdo do é simplificado por
Mas o que acontece no gráfico de quando se aproxima de pela direita?
tende a , não é?
Isso pode ser trazido para o nosso limite
Quando tende a (pela direita), o conteúdo do tende a e quando o conteúdo tende a positivamente, tende a , logo
É isso! Entendeu tudo? Responde Aí!