Determine o maior conjunto no qual a função é contínua.
36 –
Passo 1
E aí, pessoal. Tudo bem?
Aqui nessa questão nós vamos responder qual é o maior conjunto onde essa função dada é contínua.
Para achar o maior conjunto no qual é contínua, basta olhar para onde não está definida em . Com isso, o maior conjunto onde ela é contínua será o seu domínio.
Tranquilo? Vem comigo então!
Passo 2
Seja a função
Sabemos que
,
já que está dentro da raiz.
Note que essa inequação acima define um plano em . Esse plano tem vetor normal na direção
Portanto, a função será contínua para pontos “acima” desse plano, no mesmo sentido do vetor normal a ele.
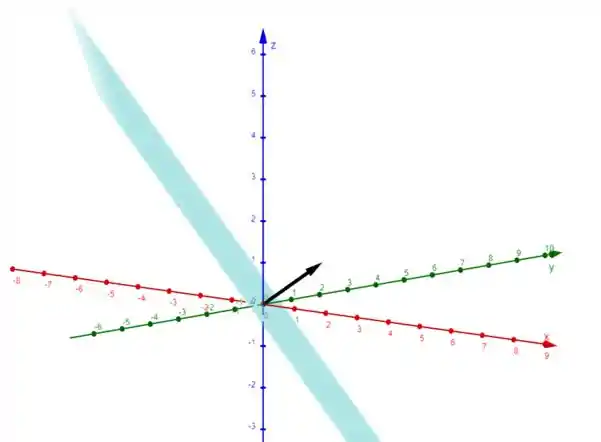
Assim, é contínua no intervalo .
Resposta
é contínua no intervalo .