Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.2 - Ex. 32
Determine o maior conjunto no qual a função é contínua
32-
Passo 1
Olá, pessoal! Tudo certo?
Aqui nessa questão nós temos que analisar a função dada e dizer quando ela é contínua ou não. Vamos fazer isso analisando o domínio da função
Beleza? Vamos lá.
Passo 2
A função é contínua para qualquer valor de e de , porém a função é contínua somente para valores de iguais a:
Dessa forma o domínio da função será:
Só que não tem como a função ser negativa até por que e estão elevadas ao quadrado logo a imagem ficará da seguinte maneira:
O que nos mostra que a imagem é um círculo de raio igual a e centro na origem.
Para você conseguir ver, esse é o gráfico da função:
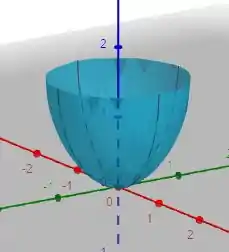
Resposta
Domínio:
Exercícios de Livros Relacionados
22.Verificar se as funções dadas são contínuas nos pontos indicados:d) f x , y =y 4 + 3 x 2 y 2 + 2 y x 3 x 2 + y 2 2 , 0 ,x , y ≠ 0,0 x , y = 0,0,P ( 0,0 )
22.Verificar se as funções dadas são contínuas nos pontos indicados:g) f x , y =y 2 + 2 x y 2 - 2 x , 0 ,x , y ≠ 0,0 x , y = 0,0,P ( 0,0 )
28. Analisar a continuidade das seguintes funções vetoriais: b) g → x , y , z = ( x ,y sen y , x z 2 sen 1 z x , y s e ny ,0 ,z ≠ 0 z = 0
28. Analisar a continuidade das seguintes funções vetoriais: f → x , y = ( x y ,x 2 - y 2 ,2 )
22.Verificar se as funções dadas são contínuas nos pontos indicados:a) f x , y =x s e n 1 y ,y ≠ 0 0 ,y = 0,P ( 0,0 )