Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 15
Determine e faça o esboço do domínio da função.
Passo 1
Olá, meu brother.
Queremos determinar o domínio de , sendo ela:
Ou seja, queremos saber que valores de , que podem ser usados para que seja real.
Para definir o domínio é melhor olharmos para as restrições. Algumas funções que utilizamos diariamente possuem restrições, as frações não podem ter zero no seu denominador, então é em relação a isso que iremos trabalhar.
Passo 2
Dada:
Essa função é definida somente se:
Ou até mesmo se:
Assim, o domínio de é
A gente reconhece esse gráfico com um gráfico de uma circunferência com raio de , mas caso esteja com dificuldades para ver isso, irei te ajudar.
Encontraremos os pontos em que nossa função toca os eixos. Fazemos isso zerando uma das variáveis:
E agora para :
Esse domínio nos dá o gráfico:
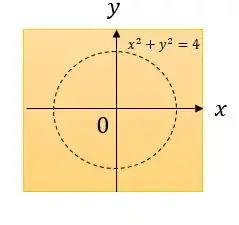
Isso é, todos os pontos na fronteira dessa circunferência não podem ser utilizado na nossa função.