Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.4 - Ex. 5

Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ .

D é uma região triangular com vértices 0 ,   0 ,   2 ,   1 ,   0 ,   3 ; ρ x ,   y = x + y

Passo 1

E aí, pessoal! Tudo numa boa?

A questão quer a massa m e o centro de massa x - ,   y - da lâmina com densidade:

ρ x , y = x + y Ocupando a região D , onde:

D é a região triangular com vértices 0 ,   0 ,   2 ,   1 ,   0 ,   3

Para encontrar a massa da lâmina aplicamos a integral:

m = ∬ D ρ x , y d A

E para o centro de massa precisamos achar o valor de:

x - = M y m

E:

y - = M x m

Onde os momentos M são dados pelas integrais:

M y = ∬ D x ρ x , y d A

M x = ∬ D y ρ x , y d A

Então, nosso objetivo é calcular essas 3 integrais, primeiro calculando seus limites de integração, que vamos tirar da região D . Lembrando que:

d A = d x   d y

Vamo lá!

Passo 2

Viu como todas a integrais que vamos calcular precisa dos limites de integração da região D ? Vamos esboçar essa região para entendermos seu comportamento para cada variável:

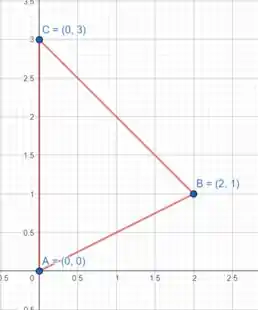
Região D

Vamos expressar essa região como uma região do Tipo I , onde x está entre duas constantes e y está dentre duas funções:

0 ≤ x ≤ 2

Como a reta que liga A e B é:

y = x 2

E a reta que liga B e C é:

y = 3 - x

Então:

x 2 ≤ y ≤ 3 - x

Agora temos nossos limites e podemos calcular nossas integrais.

Passo 3

Galera, primeiro vamos calcular a massa:

m = ∬ D   ρ x ,   y   d A = ∫ 0 2 ∫ x 2 3 - x x + y   d y   d x

Integrando primeiro em y , tratando x como constante:

= ∫ 0 2 x y + y 2 2 x 2 3 - x   d x

Aplicando os limites de y :

= ∫ 0 2 x 3 - x + 3 - x 2 2 - x . x 2 - x 2 2 2   d x =

Simplificando os termos:

∫ 0 2 - 9 8 x 2 + 9 2   d x

Agora integrando em x temos:

= - 3 x 3 8 + 9 x 2 0 2

Aplicando os intervalos de integração:

m = - 3 + 9 = 6

Passo 4

Agora vamos calcular x - , pra saber qual é o centro de massa x - ,   y - :

x - = M y m

onde M y é o momento em relação ao eixo y , calculado da seguinte forma:

M y = ∬ D   x   ρ x ,   y   d A = ∫ 0 2 ∫ x 2 3 - x x 2 + x y   d y   d x

Integrando primeiro em y , tratando x como constante:

= ∫ 0 2 x 2 y + x y 2 2 x 2 3 - x   d x

Aplicando os intervalos de integração:

= ∫ 0 2 x 2 3 - x + x 3 - x 2 2 - x 2 . x 2 - x x 2 2 2   d x

Simplificando:

= ∫ 0 2 - 9 8 x 3 + 9 x 2   d x

Integramos em x e aplicamos seus limites de integração:

= - 9 x 4 32 + 9 x 2 4 0 2 = - 9 2 + 9

x - = 9 2

Então nosso x - será:

x - = 9 2 6 = 3 4

Passo 5

Show! Agora só falta calcular y - , mas primeiro, vamos calcular o momento M x em relação ao eixo x :

M x = ∬ D   y   ρ x ,   y   d A = ∫ 0 2 ∫ x 2 3 - x x y + y 2   d y   d x

Integrando primeiro em y , tratando x como constante:

= ∫ 0 2 x y 2 2 + y 3 3 x 2 3 - x   d x

Aplicando os intervalos de integração:

= ∫ 0 2 x 3 - x 2 2 + 3 - x 3 3 - x x 2 2 2 - x 2 3 3   d x

Simplificando:

= ∫ 0 2 9 - 9 x 2   d x

Integramos em x e aplicamos seus limites de integração:

= 9 x - 9 x 2 4 0 2 = 18 - 9

Então:

y - = 9

Podemos substituir na equação:

y - = M x m

Para termos:

y - = 9 6 = 3 2

Então, nossa coordenada de centro de massa será:

x ,   - y - = 3 4 , 3 2

Resposta

m = 6

x ,   - y - = 3 4 , 3 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área da superfície.A parte da superfície z = 1 + 3 ⋅ x + 2 ⋅ y 2 que está acima do triângulo com vértices (0,0), (0,1) e (2,1).
Determine a área da superfície.A parte do paraboloide z = 4 - x 2 - y 2 que está acima do plano x y .
Determine, com precisão de quatro casas decimais, a área da parte da superfície z = 1 + x 2 y 2 que está acima do disco x 2 + y 2 ≤ 1 .
Determine a área da superfície.A parte do cilindro y 2 + z 2 = 9 que está acima do retângulo com vértices ( 0,0 ) , ( 4,0 ) , ( 0,2 ) e ( 4,2 ) .
Determine a área da superfície.A parte do plano 3 x + 2 y + z = 6 que está no primeiro octante.