Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.6 - Ex. 6

Determine a área da superfície.

A parte do paraboloide z = 4 - x 2 - y 2 que está acima do plano x y .

Passo 1

Oi, tudo certo?? Vamos ver nessa questão?

Precisamos calcular a área de uma superfície, que é parte de um paraboloide.

Pra isso, a gente usa a fórmula pra área de um gráfico z = f x , y :

A S = ∬ D f x 2 + f y 2 + 1   d A

Então primeiro vamos ter que definir quem é f x , y , pra calcular as derivadas parciais.

Depois, vamos ver qual o domínio D e calcular a integral.

Passo 2

Como a superfície é definida por

z = 4 - x 2 - y 2

Nossa função é essa

f x , y = 4 - x 2 - y 2

Então calculamos as derivadas parciais. Primeiro em função de x , com y constante:

f x = ∂ 4 - x 2 - y 2 ∂ x = - 2 x

Depois em função de y , com x constante:

f y = ∂ 4 - x 2 - y 2 ∂ y = - 2 y

Colocando na integral:

A S = ∫ ∫ D - 2 x 2 + - 2 y 2 + 1 ⋅ d A

A S = ∫ ∫ D 4 x 2 + 4 y 2 + 1 ⋅ d A

Passo 3

Agora precisamos definir que é o domínio D , pra calcular a integral.

Vamos olhar pra nossa superfície, que é a parte de um paraboloide na parte positiva de z (acima do plano x y ):

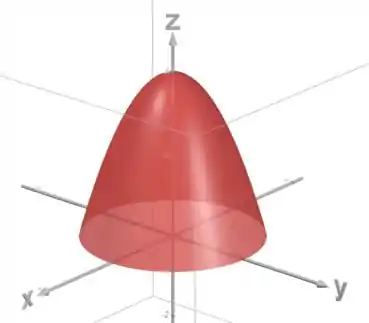
O domínio D é a projeção dessa superfície no plano x y , isso vai ser um círculo:

Então, pra resolver nossa integral, vamos fazer uma mudança de variável para coordenadas polares:

x = r cos ⁡ θ y = r sen ⁡ θ

Onde 0 ≤ r ≤ 2 e 0 ≤ θ ≤ 2 π

Quando fazemos essa mudança, temos que:

x 2 + y 2 = r 2 cos 2 ⁡ θ + r 2 sen 2 ⁡ θ = r 2

Além disso, o jacobiano é

J = r

Então:

A S = ∬ D 4 x 2 + 4 y 2 + 1   d A

= ∬ D 4 ( x 2 + y 2 ) + 1   d A =

Mudando as variáveis:

= ∫ 0 2 ∫ 0 2 π 4 r 2 + 1 ∙ r d θ d r

Passo 4

Agora basta resolver a integral iterada (sempre de dentro pra fora):

A S = ∫ 0 2 ∫ 0 2 π 4 r 2 + 1 ∙ r d θ d r =

Integrando primeiro em função de θ , mantendo r constante. Como o integrando todo depende só de r , podemos tirar da primeira integral:

= ∫ 0 2 4 r 2 + 1 ∙ r ∫ 0 2 π d θ d r =

Então:

= ∫ 0 2 4 r 2 + 1 ∙ r ∙ θ 0 2 π d r =

= ∫ 0 2 4 r 2 + 1 ∙ r ∙ 2 π d r =

Por último, vamos integrar em função de r , podemos tirar o 2 π da integral:

= 2 π ∫ 0 2 4 r 2 + 1 ∙ r d r =

Pra integrar em função de r , vamos fazer uma substituição u = 4 r 2 + 1 :

d u = 8 r d r ⇒ r d r = 1 8 d u

u 0 = 1

u 2 = 17

A integral fica assim:

= 2 π ∫ 1 17 u ∙ 1 8 d u =

A primitiva de u = u 1 2 é:

u 3 2 3 2 = 2 3 u 3 2

Então resolvendo a integral:

= 2 π ∙ 1 8 ∙ 2 3 u 3 2 1 17 =

= 2 π ∙ 1 12 ∙ u 3 2 1 17 =

Substituindo nos limites de integração:

= π 6 ∙ 17 3 2 - 1

Achamos o valor da área:

A S = π 6 17 17 - 1

Resposta

A S = π 6 17 17 - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A fronteira de uma lâmina consiste nos semicírculos y = 1 - x 2 e y = 4 - x 2 juntamente com as partes do eixo x que os une. Encontre o centro de massa da lâmina se a densidade em qualquer ponto é pro
Encontre o centro de massa da lâmina do Exercício 13 se a densidade em qualquer ponto for inversamente proporcional à sua distância da origem.
Encontre o centro de massa de uma lâmina em forma de triângulo retângulo isósceles, com os lados iguais tendo comprimento a , se a densidade em qualquer ponto for proporcional ao quadrado da sua distâ
Uma lâmina ocupa a parte do disco x 2 + y 2 ≤ 1 no primeiro quadrante. Determine o centro de massa se a densidade em qualquer ponto for proporcional à distância do ponto ao eixo x .
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é uma região triangular com vértices 0 ,0 ,2 ,1 ,0 ,3 ; ρ x ,y = x + y