Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.6 - Ex. 4

Determine a área da superfície.

A parte da superfície z = 1 + 3 ⋅ x + 2 ⋅ y 2 que está acima do triângulo com vértices (0,0), (0,1) e (2,1).

Passo 1

E aí, pessoal! Como vão?

A questão pede pra gente achar a área da superfície do plano:

z = 1 + 3 x + 2 y 2

que cruza acima do triangulo com vértices 0,0 ,   0 , 1   e   2 , 1 .

A área da superfície com a equação z = f x , y é:

A S = ∫ ∫ D ∂ z ∂ x 2 + ∂ z ∂ y 2 + 1 ⋅ d A

Ou seja, vamos achar as derivadas parciais de x e y da fun��ão:

z = 1 + 3 x + 2 y 2

  • ∂ z ∂ x : derivada da nossa função em relação a x , onde tratamos as outras variáveis como constantes.
  • ∂ z ∂ y : derivada da nossa função em relação a y , onde tratamos as outras variáveis como constantes.

    • E também vamos precisar dos limites de integração da função que é dado pela região D no plano x y .

    Lembrando também que:

    d A = d x   d y = d y   d x

    Depois de acharmos as derivadas parciais e os limites de integração, é só a gente resolver a integral dupla daquele jeito que sabemos, começando pela integral “de dentro”.

    Bora lá!

    Passo 2

    Temos então que encontrar as derivadas parciais ∂ z ∂ x e ∂ z ∂ y . Temos que:

    z = 1 + 3 x + 2 y 2

  • ∂ z ∂ x :

    • z = 1 + 3 x + 2 y 2

    Derivando em relação a x , tratamos o termo de y como constante.

    ∂ z ∂ x = 3

  • ∂ z ∂ y :

z = 1 + 3 x + 2 y 2

Derivando em relação a y , tratamos o termo de x como constante.

∂ z ∂ y = 4 y

Com isso, temos:

A S = ∫ ∫ D ∂ z ∂ x 2 + ∂ z ∂ y 2 + 1 ⋅ d A = ∬ 2 2 + 4 y 2 + 1   d A

Passo 2

Nossa região D   no plano x y é descrita por:

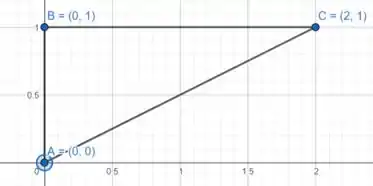
Vamos começar calculando a reta que liga o ponto (0,0) ao ponto (2,1). Usando a equação da reta chegamos que a reta que liga esses dois pontos é y = 1 2 ⋅ x . Vamos manter y fixo e variar o x . Assim, chegamos que nossos intervalos serão

0 ≤ x ≤ 2 ⋅ y

0 ≤ y ≤ 1

Aplicando os limites de integração que acabamos de encontrar, temos:

A S = ∬ 2 2 + 4 y 2 + 1   d A = ∫ 0 1 ∫ 0 2 ⋅ y 3 2 + 4 ⋅ y 2 + 1 ⋅ d x ⋅ d y

Fazendo a soma dos termos dentro da raiz:

= ∫ 0 1 ∫ 0 2 ⋅ y 10 + 16 ⋅ y 2 ⋅ d x ⋅ d y

Vamos começar a integrar em relação a x que é a integral de dentro:

∫ 0 1 10 + 16 ⋅ y 2   x 0 2 y d y

Aplicando os limites de integração:

= ∫ 0 1 10 + 16 ⋅ y 2 ⋅ 2 ⋅ y ⋅ d y  

Agora vamos resolver a integral que restou. Usando a substituição u = 16 ⋅ y 2 + 10 ficamos com a seguinte integral

1 16 ⋅ ∫ 10 26 u ⋅ d u

Calculando a integral, temos:

1 16 ⋅ ∫ 10 26 u ⋅ d u = 1 16 ⋅ 2 3 u 3 2 10 26

Aplicando os limites de integração:

= 1 24 ⋅ 26 3 2 - 10 3 2

Então:

A S = ∫ 0 1 ∫ 0 2 ⋅ y 3 2 + 4 ⋅ y 2 + 1 ⋅ d x ⋅ d y = 1 24 ⋅ 26 3 2 - 10 3 2

Resposta

A S = 1 24 ⋅ 26 3 2 - 10 3 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D = x ,y0 ≤ x ≤ 2,- 1 ≤ y ≤ 1 }; ρ ( x ,y ) = x y 2
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D = x ,y0 ≤ x ≤ a,0 ≤ y ≤ b }; ρ ( x ,y ) = c x y
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D = x ,y 0 ≤ y ≤ s e n π x L,0 ≤ x ≤ L }; ρ ( x ,y ) = y
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é delimitada pelas parábolas y = x 2 e x = y 2 ; ρ x ,y = x
Determine o centro de massa da lâmina do Exercício 11 se a densidade em qualquer ponto for proporcional ao quadrado da distância do ponto à origem.