Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.6 - Ex. 5
Determine a área da superfície.
A parte do cilindro que está acima do retângulo com vértices , , e .
Passo 1
E aii, galera?
Vamos dar uma olhada nessa questão.
Precisamos calcular a área de uma superfície, que é um cilindro .
Pra achar o valor da área do gráfico de uma função , em um domínio , podemos usar a fórmula:
Então nosso passo a passo vai ser: determinar quem é , calcular as derivadas parciais, e substituir na fórmula. Daí, vamos calcular a integral.
Passo 2
Como nossa superfície é parte do cilindro , vamos isolar o , pra definir quem é a função :
O problema disse pra gente que é a parte acima do retângulo (que faz parte do plano ), então estamos na parte positiva de :
Agora vamos calcular as derivadas parciais. Lembrando que quando derivamos em função de uma variável, as outras são constantes:
Pra derivar em função de , vamos usar a regra da cadeia:
Como a derivada de é :
Então:
Voltando pra fórmula:
Resolvendo:
Passo 3
Agora vamos ver quem é .
Nosso domínio é uma região retangular:
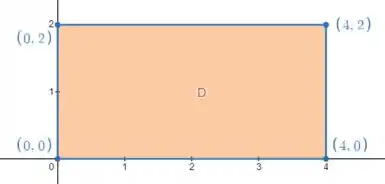
Então nossos limites de e são dados por:
Transformando nossa integral em uma integral iterada:
Passo 4
Agora vamos calcular a integral iterada, de dentro pra fora. Primeiro integramos em função de , considerando constante:
Pra conseguir resolver essa integral, vamos mexer um pouco nesse termo dentro da raiz:
Vamos transformar isso em uma fração só:
Então o termo fica assim:
Voltando pra integral:
Essa integral tá com uma cara parecida com essa daqui:
Então vamos fazer ela ficar igual. Primeiro colocamos o em evidência na raiz:
Simplificando:
Agora vamos fazer uma substituição :
Então:
Podemos tirar o da integral, e integrar em função de :
Agora substituindo nos limites de integração:
Passo 5
Por último, vamos integrar em função de . Como é constante, ele sai da integral e podemos calcular:
Resolvendo:
E a área da superfície fica: