Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.5 - Ex. 3

Determine

∮ C x 2 + y + 2 x y 3 d x + 5 x + 3 x 2 y 2 + y   d y

onde C é a reunião das curvas C 1 ,   C 2 e C 3 dadas por C 1 : x 2 + y 2 = 1 ,   y ≥ 0 ; C 2 : x + y + 1 = 0 , - 1 ≤ x ≤ 0 ; C 3 : x - y - 1 = 0 , 0 ≤ x ≤ 1 . Especifique a orientação escolhida.

Passo 1

Antes de mais nada, vamos tentar construir essas curvas dadas!

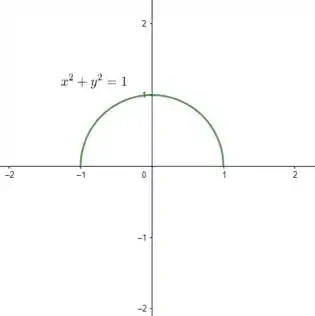
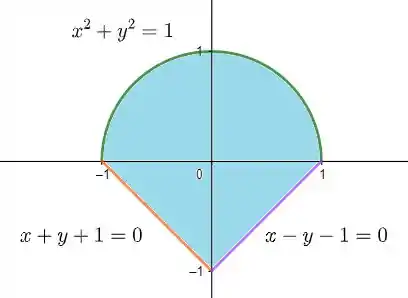
  • C 1 é dada por x 2 + y 2 = 1 com a condição y ≥ 0 . Sabe-se que x 2 + y 2 = 1 representa uma circunferência de raio r = 1 e centro 0,0 . A condição y ≥ 0 nos garante que queremos apenas os valores de y positivos!

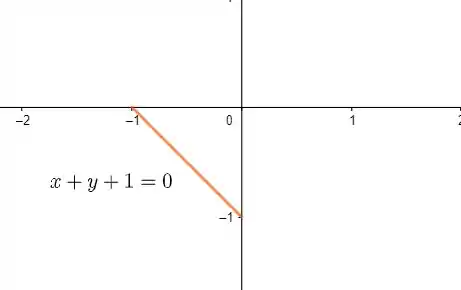
  • C 2 é dada por x + y + 1 = 0 com a condição - 1 ≤ x ≤ 0 . Assim, vemos que C 2 é o segmento de reta que passa pelos pontos - 1,0 e 0 ,   - 1 . Veja:

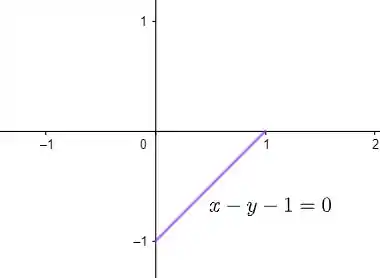
  • C 3 é dado por x - y - 1 = 0 , com a condição 1 ≤ x ≤ 0 . Assim, vemos que C 3 é o segmento de reta que passa por 1,0 e 0 ,   - 1 . Veja:

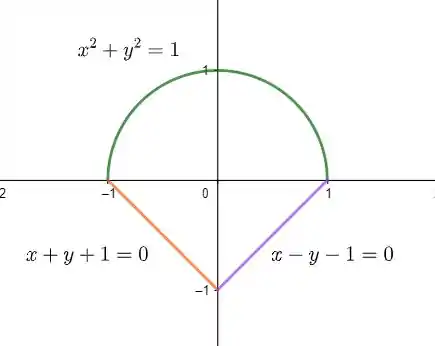
    • Juntando essas nossas três regiões, temos

    Podemos calcular essa integral de linha diretamente pela definição; porém, uma outra saída será usar o teorema de Green. Tal teorema afirma que se tomarmos a orientação positiva para C , então será válida a igualdade:

    ∮ C F 1   d x + F 2   d y = ∬ D ∂ F 2 ∂ x - ∂ F 1 ∂ y d x d y

    onde D é a área interna da região. Veja a figura abaixo:

    Passo 2

    Para a nossa integral, temos:

    F 1 = x 2 + y + 2 x y 3 F 2 = 5 x + 3 x 2 y 2 + y

    Logo,

    ∂ F 2 ∂ x = ∂ ∂ x 5 x + 3 x 2 y 2 + y ∂ F 2 ∂ x = ∂ ∂ x 5 x + ∂ ∂ x 3 x 2 y 2 + ∂ ∂ x y ∂ F 2 ∂ x = 5 + 6 x y 2 + 0 ∂ F 2 ∂ x = 5 + 6 x y 2

    Também,

    ∂ F 1 ∂ y = ∂ ∂ y x 2 + y + 2 x y 3 ∂ F 1 ∂ y = ∂ ∂ y x 2 + ∂ ∂ y y + ∂ ∂ y 2 x y 3 ∂ F 1 ∂ y = 1 + 6 x y 2

    Logo, temos que

    ∮ C x 2 + y + 2 x y 3 d x + 5 x + 3 x 2 y 2 + y   d y = ∬ D 5 + 6 x y 2 - 1 - 6 x y 2 d x d y ∮ C x 2 + y + 2 x y 3 d x + 5 x + 3 x 2 y 2 + y   d y = 4 ∬ D   d x   d y

    Passo 3

    Agora, note o seguinte:

    ∬ D d x   d y = á r e a   d a   r e g i ã o   D

    A área da região D será a área pintada em azul na figura acima. Note que

    á r e a   d a   r e g i ã o   D = á r e a   d o s   t r i â n g u l o s + á r e a   d o   s e m i c í r c u l o

  • Área de cada triângulo: A = 1 2 b a s e × a l t u r a = 1 2 1 1 = 1 2 .

    • Como temos dois triângulos, então a área total será 1 2 × 2 = 1 .

  • Área da semicircunferência: A = 1 2 π r 2 = 1 2 π 1 2 = π 2

Assim, temos

∮ C x 2 + y + 2 x y 3 d x + 5 x + 3 x 2 y 2 + y   d y = 4 1 + π 2 ∮ C x 2 + y + 2 x y 3 d x + 5 x + 3 x 2 y 2 + y   d y = 4 + 2 π

Resposta

4 + 2 π .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Complete a demonstração do Teorema de Green demonstrando a Equação 3.
Use o teorema de Green para calcular ∫ C F ⋅ d r . (Verifique a orientação da curva antes de aplicar o teorema.) F x , y = y 2 cos ⁡ x , x 2 + 2 y sen ⁡ x C é o triangulo de 0,0 �� ��a ( 2,6 ) a 2,0 a
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C x yd x + x 2 d y C é o retângulo com vértices 0,0 ,3,0 , 3,1 , ( 0,1 )
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C x yd x + x 2 y 3 d y C é o triangulo com vértices 0,0 ,1,0 e 1,2
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C cos ⁡ y d x + x 2 sin ⁡ y d y C é o retângulo com vértices 0,0 , 5,0 ,5,2e0,2 .