Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.2 - Ex. 32

(a) Determine o ponto de intersecção das retas tangentes à curva r t = ( s e n   π t ,   2   s e n   π t , cos ⁡ π t )   nos pontos t = 0 e t = 0,5 .

(b) Ilustre traçando o gráfico da curva e ambas as tangentes.

Passo 1

Fala ai pessoal, belezinha?

Nesta questão precisamos encontrar o ponto de intersecção entre duas retas, para isso teremos que encontrar as equações das retas tangentes, assim poderemos igualar as equações e encontrar o ponto de intersecção.

Mãos a obra! 😊

Passo 2

A primeira coisa a se fazer é obter o obter o vetor posição r ( t ) nos pontos de tangência t = 0 e t = 1 2 . Para isso basta substituir os valores do parâmetro t na equação da curva.

r 0 = ( s e n   0 ,   2   s e n   0 , cos ⁡ 0 ) = ( 0,0 , 1 )  

r 1 2 = s e n π 2 ,   2   s e n π 2 , cos ⁡ π 2   = ( 1 ,   2 ,   0 )

Passo 3

O segundo passo é calcular a derivada de r ( t ) que representa a equação geral do vetor tangente a esse curva.

r ' t = ( π cos ⁡ π t , 2 π cos ⁡ π t ,   - π   s e n   π t )

Logo, nos pontos de tangência t = 0 e t = 1 / 2 , os vetores tangentes serão dados por

r ' 0 = (   π cos ⁡ 0,2 π cos ⁡ 0 ,   - π   s e n   0 ) = ( π ,   2 π ,   0 )

r ' 1 2 = π cos ⁡ π 2 , 2 π cos ⁡ π 2 ,   - π   s e n π 2 = ( 0 ,   0 ,   - π )

Passo 4

Agora que sabemos os pontos e os vetores de tangência é possível calcular as equações das retas tangentes à curva nos pontos dados.

- Para t = 0 é a reta que parte do vetor posição r ( 0 ) da curva e tem a direção do vetor tangente r ' ( 0 ) . Portanto, chamando essa reta de s ( u ) , temos:

s u = r 0 + u r ' 0 = 0,0 , 1 + u π ,   2 π ,   0 = ( π u ,   2 π u ,   1 )  

- Para t = 1 / 2 é a reta que parte do vetor posição r ( 1 / 2 ) da curva e tem a direção do vetor tangente r ' ( 1 / 2 ) . Portanto, chamando essa reta de w ( v ) , temos:

w v = r 1 / 2 + v r ' 1 2 = 1,2 , 0 + v 0 ,   0 ,   - π = ( 1 ,   2 ,   - π v )

Passo 5

As retas se interceptam quando s u = w ( v ) , ou seja:

π u ,   2 π u ,   1 = ( 1 ,   2 ,   - π v )

Logo, o ponto de intersecção da reta é ( 1 ,   2 ,   1 ) .

De fato, esse ponto é comum às duas retas é obtido em s ( 1 / π ) e w ( - 1 / π ) .

Passo 6

Vamos agora esboçar o gráfico utilizando um software (google Colab)

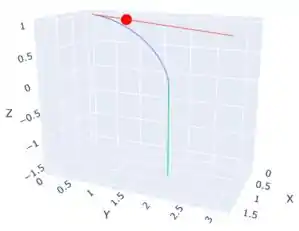
Resposta

a) P = ( 1 ,   2 ,   1 )

b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize a regra de Simpson com n = 10 para aproximar o comprimento do arco de r t = ti + t 2j + t 3k a partir da origem ao ponto (2, 4, 8)
Nos Exercícios 11-14, encontre o parâmetro de comprimento de arco ao longo da curva a partir do ponto em que t = 0, avaliando a integral s = ∫ 0 t v τ d τ da Equação 3. Em seguida, encontre o comprime
(Continuação do Exercício 19.) Encontre o vetor tangente unitário à involuta do círculo no ponto P(x, y).
Comprimento da hélice O comprimento 2 π 2 da volta da hélice no Exemplo 1 também é o comprimento da diagonal de um quadrado com 2 π unidades de lado. Mostre como obter esse quadrado cortando e aplaina
Nos Exercícios 11-14, encontre o parâmetro de comprimento de arco ao longo da curva a partir do ponto em que t = 0, avaliando a integral s = ∫ 0 t v τ d τ da Equação 3. Em seguida, encontre o comprime