Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 11.3 - Ex. 26

Determine se é possível atribui um número finito para representar a medida do volume do sólido formado pela rotação, em torno do eixo x , da região limitada pelo eixo x , pelo eixo y e pela curva cuja equação é y = e - 2 x . Caso seja possível, determine-o.

Passo 1

Vamos começar fazendo o esboço de y = e - 2 x

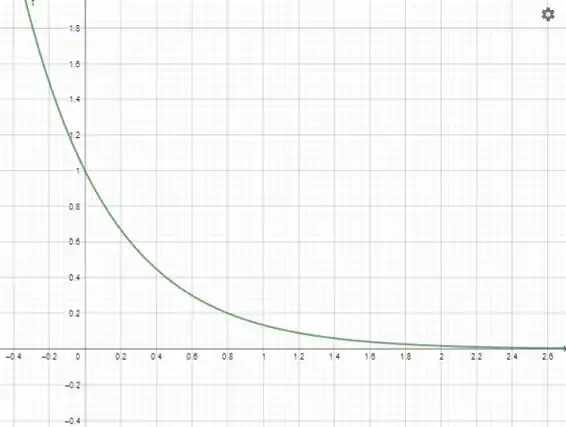
Ele quer que o volume seja a depois do eixo y . Usando discos, temos

r x = y x

E a integral vai ficar:

V = ∫ 0 + ∞ π y x 2 d x

Então a integralsera

V = ∫ 0 + ∞ π e - 2 x 2 d x = ∫ 0 + ∞ π e - 4 x d x

Passo 2

Para resolvermos essa integral imprópria, vamos fazer o seu limite

∫ 0 + ∞ π e - 4 x d x = lim b → + ∞ ⁡ ∫ 0 b π e - 4 x d x

Sabemos que

∫ π e - 4 x d x = - π 4 e - 4 x + C

Logo

lim b → + ∞ ⁡ ∫ 0 b π e - 4 x d x = lim b → + ∞ ⁡ - π 4 e - 4 x 0 b = lim b → + ∞ ⁡ - π 4 e - 4 b - - π 4 e - 4 . 0 =

lim b → + ∞ ⁡ - π 4 e - 4 b + + π 4 = - π 4 e - ∞ + π 4 = π 4

Resposta

π 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dar um exemplo de uma função f , tal que o lim b → + ∞ ⁡ ∫ - b b f x d x existe, mas a integral imprópria ∫ - ∞ ∞ f x d x é divergente.
Verificar se a integral ∫ - ∞ 0 e 5 x d x Converge. Em caso positivo, determinar seu valor.
Investigue a integral imprópria ∫ 7 ∞ 1 x - 5 2 d x
Mostrar que ∫ 1 ∞ d x x É divergente.
Encontrar a área sob a curva y = e - x ,x ≥ 0 .